Дисконтирование по простым процентным ставкам
В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды Р. Такой процесс начисления и удержания процентов называется дисконтированиемили учетом процентов, D=S-P – дисконтом, Р – современной или приведенной величиной суммы S.
Термин «дисконтирование» употребляется и в более широком смысле – как сегодняшняя (современная) стоимость Р будущей суммы S.
В зависимости от вида процентной ставки применяют два метода дисконтирования– математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения (относительный рост)
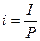 ,
,
где I – процентные деньги, Р – начальная сумма долга.
Во втором случае – учетная ставка (относительная скидка)
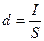 ,
,
где S – наращенная (конечная) сумма долга.
Математическое дисконтированиепредставляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды. Задача в этом случае формулируется так: какую первоначальную сумму надо выдать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i? Решение записывается формулой
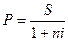 ,
,
где
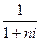 –
–
дисконтный множитель.
Банковский учет (учет векселей).Начнем с простого примера. Некто попросил в банке кредит в размере 1000000 рублей. Банкир говорит: «Пожалуйста. Учетная ставка у нас 10% годовых, так что 100000 рублей мы с Вас сейчас же удержим. Итак, получите 900000 рублей, но вернете через год, конечно, все 1000000». В этой операции все в пользу банкира. Во-первых, проценты уже удержаны. Во-вторых, доходность этой операции для банка больше, чем объявленные 10%, так как процентная ставка равна 100000/900000, что примерно составит 11,1%.
Долговая расписка, содержащая обязательство выплатить определенную денежную сумму в конкретный срок, называется векселем. Суть операции банковский учет заключается в следующем. До наступления срока платежа по векселю банк покупает его у владельца по цене, меньше указанной на векселе. При этом применяется учетная ставка
d=(S-P)/Sn,
D=Snd –
размер дисконта.
Тогда приведенная стоимость определится соотношением
P=S-Snd=S(1-nd),
где (1-nd) – дисконтный (дисконтирующий) множитель показывает долю, которую составит начальная сумма, положенная в банк под i процентов годовых, от наращенной к концу n-го года; n – срок в годах от момента учета векселя до даты уплаты по нему.
Замечание. Старинная операция учет векселя применяется и в современной финансовой практике:
- рефинансирование: один из приемов поддержки Центральным банком банка-банкрота – покупка у него портфеля векселей с их оплатой до наступления срока платежа;
- форфейтинговые операции: продавец – банк (форфетор) – покупатель (при покупке дорогостоящего оборудования).
Пример (билет № 15 для простой ставки).Через 5 лет должник выплатит кредитору сумму в размере 1000000 руб.
1) Какова первоначальная сумма, полученная должником если кредит выдан:
а) под 20 % годовых, проценты простые;
б) под 20 % годовых, проценты сложные.
2) Какую сумму получит за это обязательство кредитор, если он переуступит обязательство банку, который учтет его:
а) по простой учетной ставке 20 % годовых;
б) по сложной учетной ставке 20 % годовых.
Решение.
| n=5 лет | 1) матем. дисконтирование: |
| S=1000000 руб. | 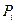 =S/(1+ni) =S/(1+ni)
|
| i=20 % | 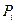 =1000000/(1+5*0.2)=500000 (руб.) =1000000/(1+5*0.2)=500000 (руб.)
|
| d=20 % | 2) банковский учет: |
1) 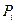
| 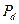 =S*(1-nd) =S*(1-nd)
|
2) 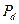
| 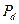 =1000000*(1-5*0.2)=0 –
дисконтный множитель при простой учетной ставке быстро убывает до 0; n=5 слишком велико для такой операции. =1000000*(1-5*0.2)=0 –
дисконтный множитель при простой учетной ставке быстро убывает до 0; n=5 слишком велико для такой операции.
|
1.2. Сложные проценты
Дата добавления: 2019-09-30; просмотров: 598;











