Наращение по сложным процентным ставкам
Определение. Процентная ставка называется сложной, если проценты выплачиваются не сразу, а присоединяются к сумме долга. База для начисления процентов не остается постоянной, а увеличивается с каждым шагом во времени. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называют капитализацией процентов.
Сложные проценты используются в долгосрочных финансово-кредитных операциях.
Наращенная сумма определяется по формуле
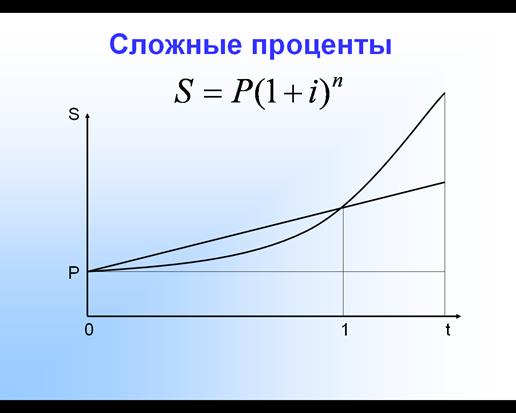
Комментарии к рисунку: наращенная сумма S изменяется в соответствии с геометрической прогрессией; в долгосрочном периоде (при n>1 г.) наращенная сумма при начислении сложных процентов растет быстрее, чем при начислении простых; если же n<1 г., то выгоднее простая процентная ставка; для n=1 г. S при начислении простых и сложных процентов будут одинаковы.
При использовании плавающей процентной ставки формула наращения примет вид:
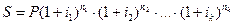 ,
,
где 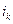 – ставка процента в периоде
– ставка процента в периоде 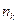 .
.
Пример (билет № 3)*[1].Кредитный договор заключен на 1 год. Первоначальная сумма равна 2000000 руб. Период начисления процентов –квартал. Определить наращенную сумму и множитель наращения для случаев:
1) применяется сложная ставка процентов, за первый квартал – 10 %, а за каждый последующий квартал на 1 % меньше;
2) применяется простая ставка процентов, за первый квартал – 10 %, а за каждый последующий квартал на 1 % меньше;
3) применяется сложная ставка – 10 %, одинаковая для всех кварталов;
4) применяется простая ставка – 10 %, одинаковая для всех кварталов.
Решение.
| N=1 | МН=S/P – самостоятельно |
| P=2 млн.руб. | 1) 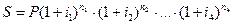
|
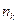 =1/4=0,25 г. =1/4=0,25 г.
|  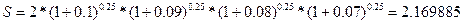
|
1) 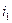 =10%, =10%, 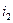 =9%,…- % сложн. =9%,…- % сложн.
| 2) 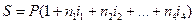
|
2) 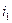 =10%, =10%, 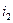 =9%,…- % прост. =9%,…- % прост.
| 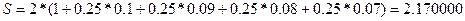
|
3) 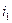 =…= =…= 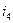 =10% - % слож. =10% - % слож.
| 3) 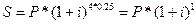 - обычное наращение по сложной ставке - обычное наращение по сложной ставке
|
4) 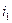 =…= =…= 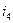 =10% - % прост. =10% - % прост.
| S=2*(1+0,1)=2.200000 |
| МН, S | 4) 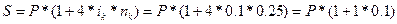 - обычное наращение по простой ставке - обычное наращение по простой ставке
|
| S=2*(1+0.1)=2.200000 | |
| Комментарий: совпадение S в п.п. 3 и 4 объясняется тем, что n=1 г. |
Дата добавления: 2019-09-30; просмотров: 705;











