Дисконтирование и учет по простым ставкам. Наращение по учетной ставке

В практике часто приходится решать задачу, обратную наращению процентов, когда по заданной сумме S, соответствующей концу финансовой операции, требуется найти исходную сумму Р. Расчет Р по S называется дисконтированием суммы S. Величину Р, найденную дисконтированием, называют современной величиной (текущей стоимостью) суммы S. Проценты в виде разности D=S-P называют дисконтом или скидкой. Процесс начисления и удержания процентов вперед (в виде дисконта) называют учетом. Дисконт как скидка с конечной суммы долга может определяться через процентную ставку или в виде абсолютной величины.

Таким образом, в практике используются два принципа расчета процентов: (1) путем наращения суммы ссуды и (2) устанавливая скидку с конечной суммы долга.

В большинстве случаев фактор времени учитывается в финансовых контрактах именно с помощью дисконтирования. Величина P эквивалентна сумме S в том смысле, что через определенный период времени и при заданной ставке процентов она в результате наращения станет равной S. Поэтому операцию дисконтирования называют также приведением. Но понятие приведения шире, чем дисконтирование. Приведение – это определение любой стоимостной величины на некоторый момент времени. Если некоторая сумма приводится к более ранней дате, чем текущая, то применяется дисконтирование, если же речь идет о более поздней дате, то – наращение (см. рис. 2).

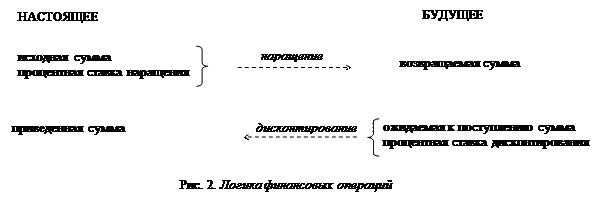Известны два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором – учетная ставка.

Математическое дисконтирование. Этот вид дисконтирования представляет собой решение задачи, обратной наращению первоначальной ссуды. Если в прямой задаче

S=P(l+ni),

то в обратной

.

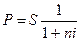Дробь в правой части равенства при величине S называется дисконтным множителем. Этот множитель показывает, какую долю составляет первоначальная сумма ссуды в окончательной величине долга. Дисконт суммы S равен D=S-P.

Пример 4. Через 145 дней после подписания договора должник выплатит 120 тыс. рублей. Кредит выдан под 15% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?

Решение. Дисконтный множитель в данном случае будет равен 1/(1+ni)=1·(1+(145/365) 0,15)=0,9438.

Первоначальная сумма долга P=120·0,9438=113,256 тыс. рублей.

Банковский или коммерческий учет. Операция учета (учета векселей) заключается в том, что банк до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца (являющегося кредитором) по цене ниже той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает (учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует процентный доход в виде дисконта. В свою очередь владелец векселя с помощью учета имеет возможность получить деньги хотя и не в полном объеме, однако ранее указанного в векселе срока.

При учете векселя применяется банковский (коммерческий) учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка, которую мы обозначим символом d.

По определению, простая годовая учетная ставка находится как

.

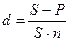Размер дисконта, или суммы учета, равен D=S·n·d; если d – годовая учетная ставка, то n измеряется в годах. Таким образом,

P=S – Snd = S·(1-nd). (1.4)

Множитель (1-nd) называется дисконтным множителем. Срок n измеряет период времени от момента учета векселя до даты его погашения. Дисконтирование по учетной ставке производится чаще всего при условии, что год равен 360 дням, число дней берется точным.

Из формулы (1.4) вытекает, что при n>1/d величина дисконтного множителя (и суммы P) станет отрицательной. Т.е. при относительно большом сроке векселя учет может привести к нулевой или отрицательной сумме P, что лишено смысла. Например, при d=20% уже 5-летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете. Такая ситуация не возникает при математическом дисконтировании: при любом сроке современная величина платежа больше нуля.

Пример 5. Вексель выдан на сумму 30 тыс. рублей со сроком погашения 1.10.2001. Владелец векселя учел его в банке 27.07.2001 по учетной ставке 12% годовых. Найти дисконтированную величину векселя.

Решение. Дисконтный множитель (1-nd)=1-(66/360)·0,12=0,978.

Дисконтированная величина векселя P=30·0,978=29,34 тыс.рублей.

Наращение по учетной ставке.Простая учетная ставка иногда применяется и при расчете наращенной суммы, т.е. для расчета S по P. В частности, в этом возникает необходимость при определении суммы, которую надо поставить в векселе, если задана текущая сумма долга. В этом случае из формулы (1.4) следует, что

.

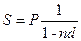Множитель наращения здесь равен 1/(1-nd). Наращение не пропорционально ни сроку, ни ставке. Надо заметить, что при n>1/d расчет лишен смысла, т.к. наращенная сумма становится бесконечно большим числом.

Пример 6. Для погашения своего долга величиной 500 тыс. рублей предприятие 11.04.2001. выдало банку вексель со сроком погашения 3.08.2001. Какова величина векселя, если учетная ставка составляет 14% годовых?

Решение. Множитель наращения 1/(1-nd)=1/(1-(114/360)·0,14)=1,0464.

Величина векселя S=500·1,0464=523,2 тыс. рублей.