Применения формулы Тейлора

а) Приближенное вычисление значений функции. Если в формуле (4) (или (5)) отбросить остаточный член, то получим приближенное значение функции

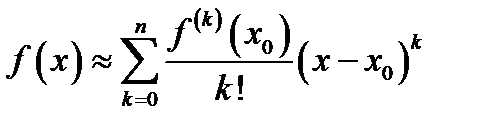
с точностью до модуля остаточного члена. Если величина 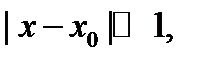то и погрешность этого приближенного равенства будет очень малой. Например, 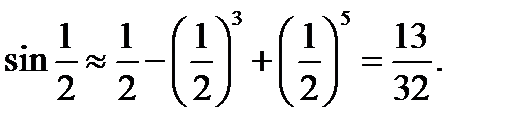При этом

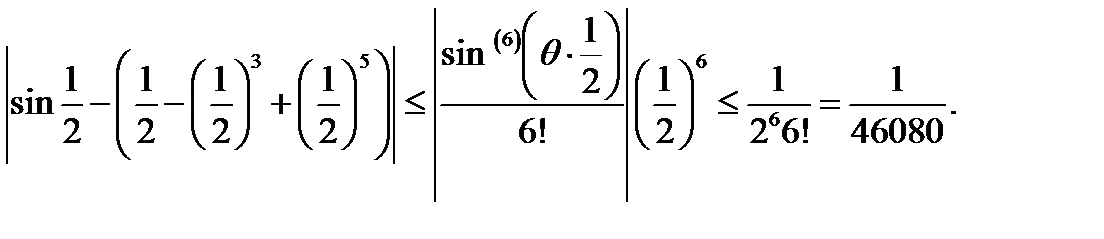
б) Вычисление пределов. Ранее мы отметили, что при вычислении предела 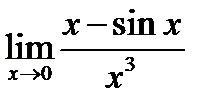не достаточно формулы эквивалентности 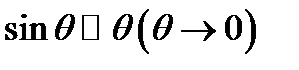, так как при использовании этой формулы не

исчезает неопределенность. В таких случаях пользуются локальной формулой Тейлора (4), записывая в ней столько слагаемых, чтобы стало возможным ликвидировать неопределенность. В нашем примере поступаем так:

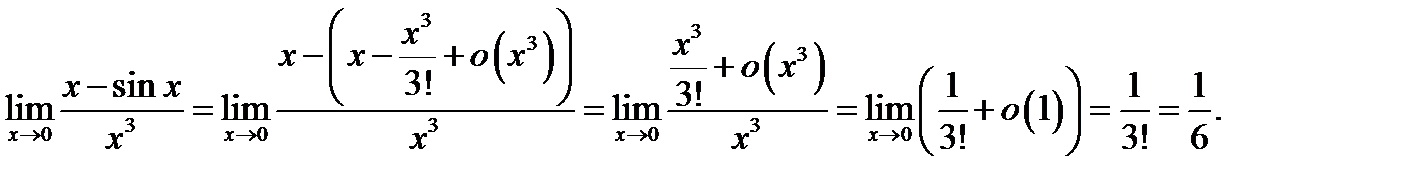
Правило Лопиталя

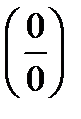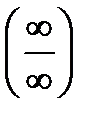Другой способ раскрытия неопределенностей типаили доставляет так называемое правило Лопиталя, к изложению которого мы переходим.

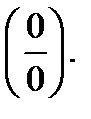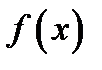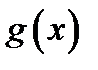Теорема Лопиталя Пусть функции и в некоторой проколотой окрестности 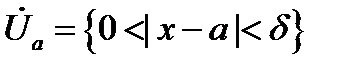удовлетворяют требованиям:

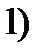
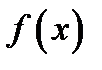и 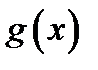непрерывны и дифференцируемы в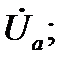

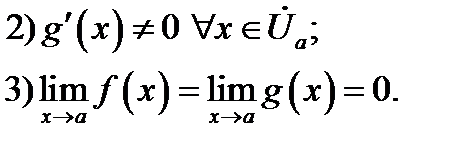
Если при этом существует(конечный или бесконечный) предел отношения производных: 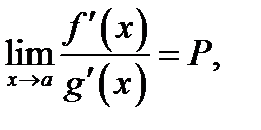то и существует равный ему предел отношения самих функций: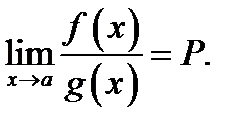

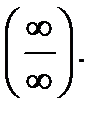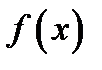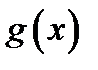Теорема Лопиталя Пусть функции и в некоторой проколотой окрестности 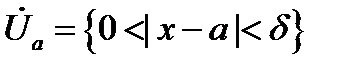удовлетворяют требованиям:

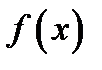и 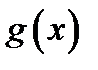непрерывны и дифференцируемы в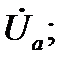

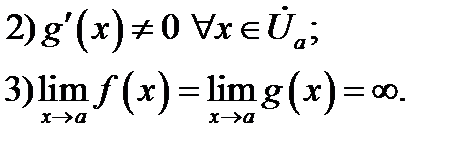
Если при этом существует (конечный или бесконечный) предел отношения производных: 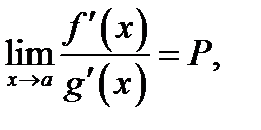то и существует равный ему предел отношения самих функций: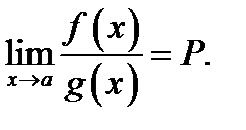

Например, для рассмотренного выше предела имеем

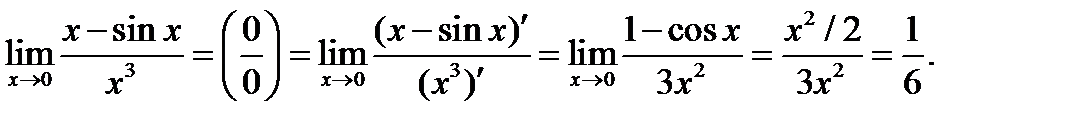
Лекция 4. Свойства функций, непрерывных на отрезке: ограниченность, достижение наибольшего и наименьшего значений, реализация всех промежуточных значений. Свойства дифференцируемой функции: монотонность, экстремумы. Схема построения графика функции с помощью первой производной