Выпуклость, вогнутость, точки перегиба
Пусть функция 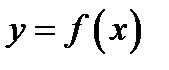 дифференцируема в точке
дифференцируема в точке 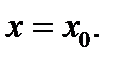 Тогда в точке
Тогда в точке 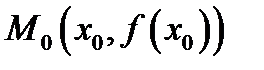 она имеет касательную, каждая точка
она имеет касательную, каждая точка 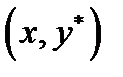 удовлетворяет уравнению
удовлетворяет уравнению
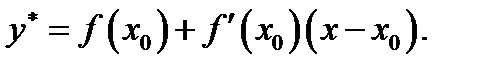
Определение 3.Говорят, что кривая 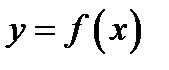 выпукла вверх в точке
выпукла вверх в точке 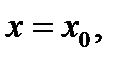 если существует
если существует 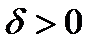 такое, что в окрестности
такое, что в окрестности 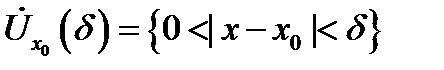 кривая
кривая 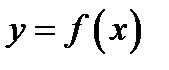 находится
находится
ниже своей касательной (3) в точке 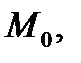 т.е. если
т.е. если 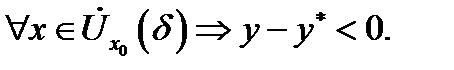 Если же
Если же 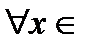
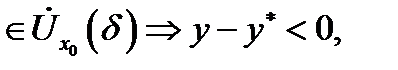 то кривая
то кривая 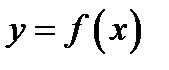 называется выпуклой вниз в точке
называется выпуклой вниз в точке 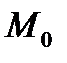 (часто говорят, о выпуклости или вогнутости в точке
(часто говорят, о выпуклости или вогнутости в точке 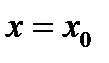 ). Говорят, что кривая
). Говорят, что кривая 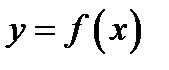 выпукла вверх (выпукла вниз) на интервале
выпукла вверх (выпукла вниз) на интервале 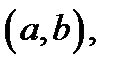 если она выпукла вверх (выпукла вниз) в каждой точке
если она выпукла вверх (выпукла вниз) в каждой точке 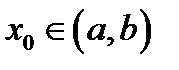 этого интервала.
этого интервала.
На рисунке Р.2 функция 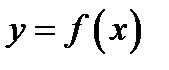 выпукла вверх в точке
выпукла вверх в точке 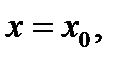 а на Р.3 – выпукла вниз.
а на Р.3 – выпукла вниз.
Теорема 3.Пусть функция 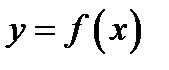 дважды дифференцируема на интервале
дважды дифференцируема на интервале 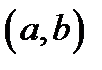 . Тогда справедливы высказывания:
. Тогда справедливы высказывания:
1. если
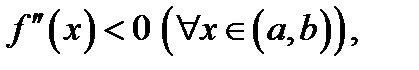 то кривая
то кривая 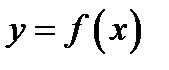 выпукла вверх на
выпукла вверх на 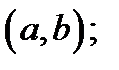
2. если 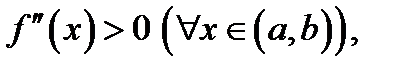 то кривая
то кривая 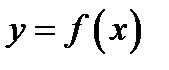 выпукла вниз на
выпукла вниз на 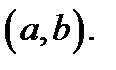
Доказательство.Пусть 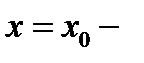 произвольная точка интервала
произвольная точка интервала 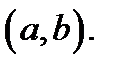 Окружим её отрезком
Окружим её отрезком 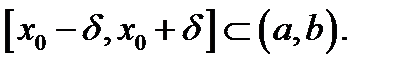 Так как функция
Так как функция 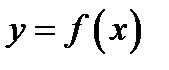 удовлетворяет на этом отрезке всем условиям теоремы Тейлора с остаточным членом в форме Лагранжа, то для всех
удовлетворяет на этом отрезке всем условиям теоремы Тейлора с остаточным членом в форме Лагранжа, то для всех 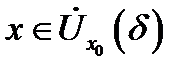 имеет место представление
имеет место представление
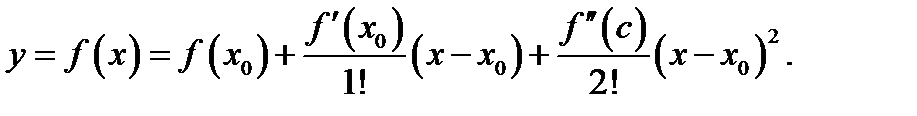
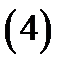
С другой стороны, в точке 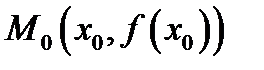 функция
функция 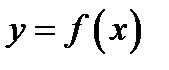 имеет касательную с уравнением
имеет касательную с уравнением 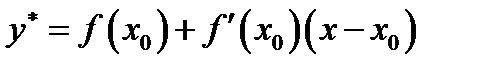 .Значит,
.Значит, 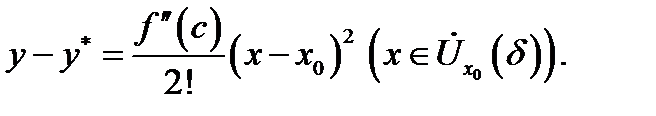 Отсюда видно, что если
Отсюда видно, что если 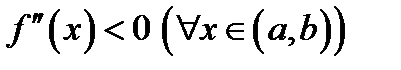 (тогда и
(тогда и 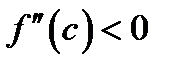 ), то
), то 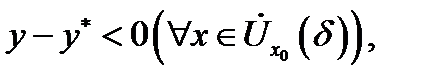 значит,
значит,
кривая 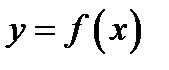 выпукла вверх в точке
выпукла вверх в точке 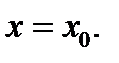 Если же
Если же 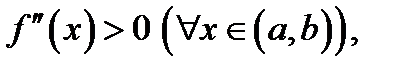 то то
то то 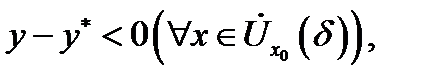 значит, кривая
значит, кривая 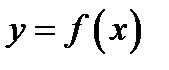 выпукла вниз в точке
выпукла вниз в точке 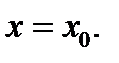 Теорема доказана.
Теорема доказана.
Определение 4.Точка 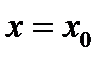 называется точкой перегиба кривой
называется точкой перегиба кривой 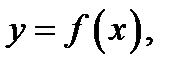 если:а)
если:а) 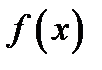 дифференцируема в точке
дифференцируема в точке 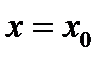 ; б) кривая
; б) кривая 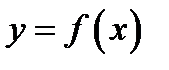 при переходе
при переходе 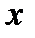 через точку
через точку 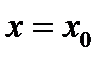 изменяет направление выпуклости (это равносильно тому, что разность
изменяет направление выпуклости (это равносильно тому, что разность 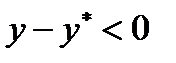 изменяет знак при переходе
изменяет знак при переходе 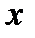 через точку
через точку 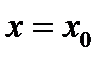 ).
).
Необходимое условие точки перегиба.Если 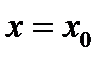 - точка перегиба и если существут
- точка перегиба и если существут 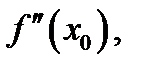 то
то 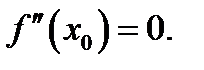
Доказательствовытекает из локальной формулы Тейлора и из равенства
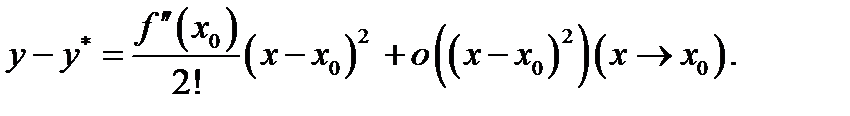
Замечание 4.К точкам, подозрительным на “перегиб”, следует отнести, прежде всего, точки 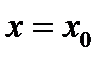 , для которых
, для которых 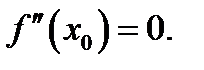 Однако “перегиб” может иметь место и в точках, в которых вторая производная
Однако “перегиб” может иметь место и в точках, в которых вторая производная 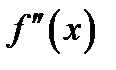 не существует или равна
не существует или равна 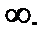 Например, в точке
Например, в точке 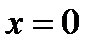 функция
функция 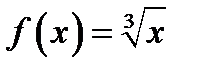 имеет производную
имеет производную 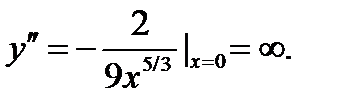 И в этой точке эта функция имеет “перегиб”. Очевиден следующий результат.
И в этой точке эта функция имеет “перегиб”. Очевиден следующий результат.
Теорема 4 (достаточное условие точки перегиба).Пусть функция 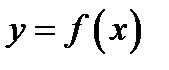 дифференцируема в точке
дифференцируема в точке 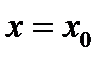 и некоторой её окрестности и дважды дифференцируема в некоторой проколотой окрестности этой точки. Тогда если при переходе
и некоторой её окрестности и дважды дифференцируема в некоторой проколотой окрестности этой точки. Тогда если при переходе 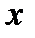 через точку
через точку 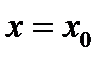 вторая производная изменяет знак, то точка
вторая производная изменяет знак, то точка 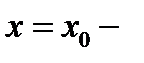 перегиба кривой
перегиба кривой 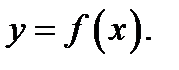
Дата добавления: 2016-06-05; просмотров: 1807;











