Задача о пропорциях потребления и накопления

Введем в рассмотрение следующие экономические показатели страны,

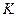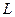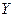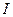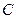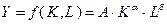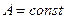предполагая, что они заданы в условных единицах: – объем производственных фондов, – объем затрат труда (в другой интерпретации – трудовые ресурсы), – национальный доход, – объем накопления, – объем потребления. Используя производственную функцию Кобба-Дугласа, запишем: , где , а постоянные 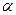и 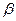удовлетворяют условию 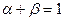. Значения 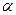(и соответственно 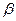) подбирают для экономики каждой конкретной страны. В частности, для экономики СССР использовались значения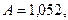 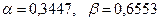. 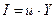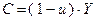Объемы накопления и потребления связаны с национальным доходом соотношениями и , где 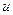– норма накопления, 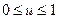. Будем рассматривать 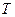периодов планирования 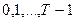; для обозначения номера периода планирования используем переменную 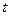, которую также можно рассматривать как номер момента времени начала очередного периода планирования. Требуется найти оптимальную стратегию планирования, т.е. стратегию, которая позволила бы иметь к моменту времени 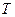производственные фонды в заданном объеме и при этом максимизировать потребление. Отметим, что средства накопления используются только на приобретение и создание производственных фондов, а влияние потребления на трудовые ресурсы в данной задаче не учитываем. В качестве управления используем норму накопления, устанавливая ее значения 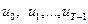в начале каждого периода планирования. Установленная норма накопления 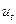действует в течение 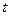-го периода планирования. Используя в качестве целевой функции суммарный за рассматриваемый период 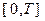объем потребления, приходящийся на единицу объема трудозатрат, с учетом рассмотренных выше зависимостей сформулируем задачу о пропорциях потребления и накопления в виде задачи динамического программирования:

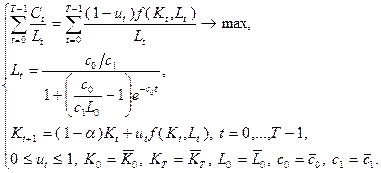(4.1.2)

Здесь 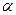(норма амортизации производственных фондов), 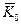, , 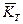, , 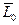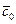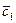– заданные величины, причем 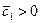, 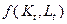– производственная функция Кобба-Дугласа. Характер зависимости объема затрат труда 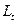от времени 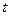для модели этой зависимости, использованной в (4.1.2), иллюстрируют графики, представленные на рис. 4.1.1. Эти графики свидетельствуют о достаточно широких воз-

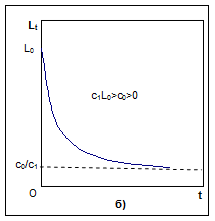
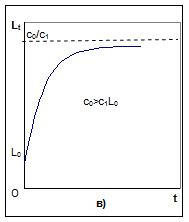
Рис. 4.1.1. Графики зависимости объема затрат труда от времени

можностях выбора варианта динамики изменения объема трудозатрат в рамках рассматриваемой модели. Такой выбор легко осуществить путем установки соответствующих значений параметров модели. Зависимости, представленные на рис. 4.1.1, могут также рассматриваться как аппроксимации трендов, выделенных в результате обработки реализаций случайных процессов, т.е. как приближенные зависимости математического ожидания от времени.