МЕТОДОМ Р. БЕЛЛМАНА

В соответствии с постановкой задачи о замене оборудования, приведенной в разд. 4.1, для функции (4.2.3) можно записать:

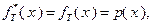(4.3.1)

где 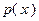– годовая прибыль, получаемая от использования оборудования возраста 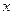. Если возраст оборудования меньше максимально допустимого значения (т.е. 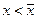), то, в соответствии с (4.2.4), запишем:

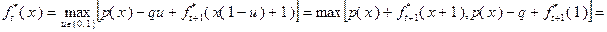
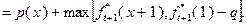(4.3.2)

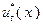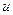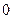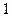Условно оптимальным управлением здесь является то из значений ( или ), на котором достигается максимум (4.3.2). Поэтому выбор того или иного управления в качестве условно оптимального определяется следующими условиями:

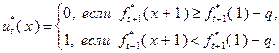(4.3.3)

Если возраст оборудования в -м календарном году равен максимально допустимому ( 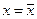), то в конце этого года однозначно происходит замена оборудования и в этом случае вместо (4.3.2) можно записать:

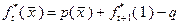, (4.3.4)

что соответствует .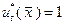

Если возраст оборудования в начальном состоянии 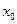не задан и существует возможность выбора оборудования разного возраста, то значение 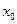может быть определено в результате решения оптимизационной задачи 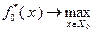. Используя 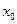и найденные условно оптимальные управления, можно получить траекторию рассматриваемой системы.

Пример 4.3.1

Рассмотрим задачу о замене оборудования (4.1.3) со следующими исходными данными: .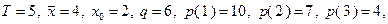

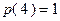В процессе решения задачи будем заполнять две таблицы: табл. 4.3.1 и табл. 4.3.2. В первую будем вносить значения функций Беллмана, во вторую – значения условно оптимальных управлений.

В соответствии с (4.3.1), последнюю строку табл. 4.3.1 заполняем значениями 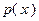, взятыми из исходных данных. Вычисление последующих значений функций 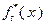, 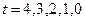при значениях аргумента 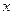, равных 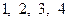, производится в соответствии с соотношениями (4.3.2) и (4.3.4), которые можно представить в следующем объединенном виде:

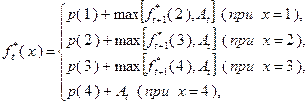(4.3.5)

где .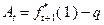

Параллельно с заполнением табл. 4.3.1 значениями функций, вычисленными с использованием выражения (4.3.5), в табл. 4.3.2 вносятся значения условно оптимальных управлений, найденных в соответствии с (4.3.3) или, что то же самое применительно к рассматриваемому примеру, с помощью следующих условий, в которых величина 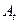имеет тот же смысл, что и в (4.3.5):

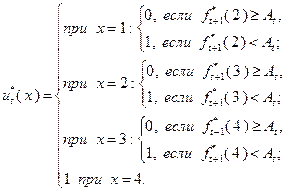
Ниже приведены расчеты значений, представленных в таблицах 4.3.1 и 4.3.2.

При : ;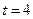

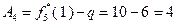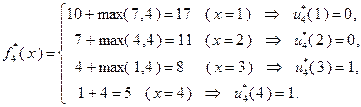
При : ;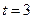

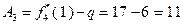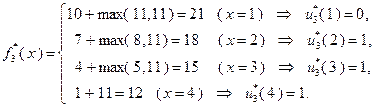
При : ;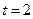

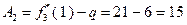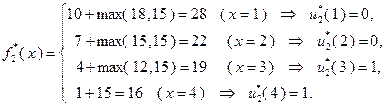
При : ;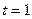

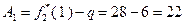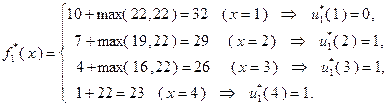
При : ;

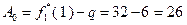Таблица 4.3.1 Таблица 4.3.2

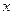
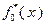
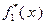
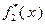
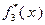
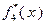
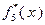
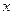
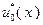
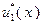
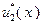
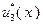
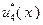
Согласно исходным данным, 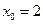, поэтому 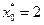. В соответствии с результатами, представленными в табл. 4.3.2, 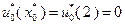. Поэтому в конце первого года работы замена оборудования не производится. В течение второго года работы возраст оборудования равен 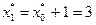, и поскольку 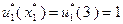, в конце второго года осуществляется замена оборудования. Следовательно, в течение третьего года возраст оборудования равен 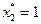, и так как 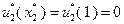, в конце третьего года замена оборудования не производится. В течение четвертого года возраст оборудования составляет 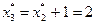, причем 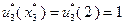, что означает замену оборудования в конце четвертого года. В течение пятого года возраст оборудования равен 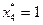и поскольку 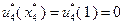, в конце пятого года замена оборудования не производится. Следовательно, в течение шестого года работы возраст оборудования составит .

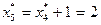В соответствии с полученными результатами, оптимальной стратегией является замена оборудования после второго и четвертого года.

ЗАКЛЮЧЕНИЕ

Математическое программирование можно рассматривать в двух аспектах – как чисто математическую теорию и как аппарат решения прикладных задач. С теоретической точки зрения математическое программирование имеет дело с задачами определенного вида, а именно с оптимизационными (или экстремальными) задачами. Специфика этих задач определяет ряд интересных теоретических результатов. Представляется, что математические объекты данного типа выявлены еще не полностью и дальнейшее развитие их теории приведет к новым интересным результатам. Прикладная ценность методов математического программирования во многом определяется возможностью решать с их помощью большое число практических задач. Наличие средств численного решения этих задач позволяет принять хорошее решение в каждом конкретном случае и оценить его последствия. Современная вычислительная техника, отличающаяся высоким быстродействием и значительными объемами памяти запоминающих устройств, дает возможность применять методы математического программирования для решения задач большой размерности в условиях жестких ограничений по времени. Выявление новых задач, допускающих оптимизационную постановку, не только способствует расширению области применения методов математического программирования, но также стимулирует развитие теории оптимизации, делая это научное направление перспективным для дальнейших исследований.

Следует отметить, что универсального метода математического программирования, наилучшего во всех отношениях, не существует. Поэтому для эффективного решения конкретной задачи следует разумно сочетать различные методы с учетом всевозможной априорной информации о решаемой задаче (гладкость целевой функции, выпуклость, физические или какие-либо иные соображения об области возможного расположения оптимальной точки и т.д.), имеющихся вычислительных средств и т.п. В ситуациях, когда нет никакой априорной информации о задаче, полезно попробовать применить не очень точные, но простые методы ее решения (например, метод перебора значений функции на сетке с небольшим числом узловых точек, метод покоординатного спуска, метод случайного поиска), а затем на основе накопленной информации при необходимости перейти к более точным методам. В тех случаях, когда пользователь, проводящий расчеты, не является компетентным в области методов решения экстремальных задач, желательно иметь прикладные компьютерные программы оптимизации, работающие в автоматическом режиме. Для этого пакет программ оптимизации должен содержать управляющую программу, обеспечивающую автоматический выбор наиболее подходящей последовательности используемых методов, их параметров в зависимости от конкретной решаемой экстремальной задачи.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Как формулируются основная, стандартная и каноническая задачи линейного программирования?

2. В чем заключается правило оптимальности в симплекс-методе?

3. Как формулируется правило отсутствия решения задачи в симплекс-методе?

4. Как выполняется расчет очередной опорной точки в симплекс-методе?

5. Какова связь между параметрами итераций в симплекс-методе?

6. Как определяется первая опорная точка в симплекс-методе?

7. Как формулируется двойственная задача в линейном программировании?

8. Как формулируется линейная задача целочисленного программирования?

9. Как формулируется транспортная задача?

10. Как формулируется задача о коммивояжере?

11. В чем заключается алгоритм Гомори?

12. В чем состоит метод ветвей и границ?

13. Какая функция называется выпуклой?

14. Как формулируется задача нелинейного программирования?

15. В чем заключаются дифференциальные критерии выпуклости функций?

16. Как функция Лагранжа используется для решения задач математического программирования?

17. В чем заключается метод покоординатного спуска?

18. В чем состоит метод случайного поиска?

19. В чем заключается градиентный метод?

20. Каково содержание метода проекции градиента?

21. В чем состоит метод линеаризации?

22. Каково содержание метода Ньютона?

23. Как формулируется задача динамического программирования?

24. Как формулируется задача о пропорциях потребления и накопления?

25. Как формулируется задача о замене оборудования?

26. Как формулируется задача о распределении ресурсов в форме задачи динамического программирования?

27. В чем заключается метод динамического программирования Р. Беллмана?