МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Р. БЕЛЛМАНА
Запишем задачу динамического программирования в виде, несколько отличающемся от (4.1.1), но по сути эквивалентном:
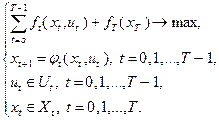 (4.2.1)
(4.2.1)
Будем считать допустимыми к использованию только управления, принадлежащие множеству допустимых управлений, которое определяется следующим образом:
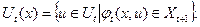 (4.2.2)
(4.2.2)
Введем функцию Беллмана 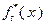 , которая при
, которая при 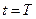 определяется выражением
определяется выражением
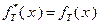 , (4.2.3)
, (4.2.3)
а при 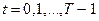 рекуррентным соотношением
рекуррентным соотношением
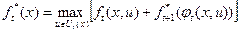 . (4.2.4)
. (4.2.4)
Выражение (4.2.4) при 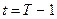 может быть записано также в виде:
может быть записано также в виде:
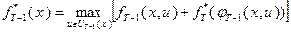 .
.
Рекуррентное соотношение (4.2.4) называется функциональным уравнением Беллмана. Функцию Беллмана обычно бывает найти сложно, что является недостатком метода динамического программирования.
Введем понятие условно оптимального управления Беллмана, представляющего собой совокупность допустимых управлений, на которых достигается максимум (4.2.4):
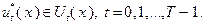
Здесь управление 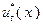 оптимально при условии, что значение
оптимально при условии, что значение 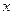 , соответствующее моменту времени
, соответствующее моменту времени 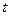 , также оптимально.
, также оптимально.
При определении условно оптимального управления и функции Беллмана в процессе решения задачи динамического программирования используются следующие формальные правила:
1) 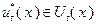 ;
;
2) 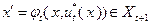 ;
;
3) 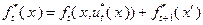 ,
,
где 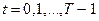 . В результате имеем функцию
. В результате имеем функцию 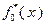 .
.
Конкретные траектории состояния и управлений системы определяют следующим образом. Сначала находят решение 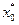 оптимизационной задачи
оптимизационной задачи 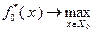 и в качестве управления в начальный момент времени используют условно оптимальное управление
и в качестве управления в начальный момент времени используют условно оптимальное управление 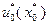 . Тогда
. Тогда 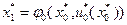 . Затем в качестве следующего управления принимают
. Затем в качестве следующего управления принимают 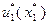 и определяют
и определяют 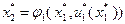 . Процесс продолжается вплоть до нахождения
. Процесс продолжается вплоть до нахождения 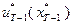 и
и 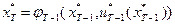 . В общем виде для процесса определения траектории системы можно записать:
. В общем виде для процесса определения траектории системы можно записать:
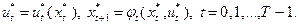
Изложенный метод построения траектории системы носит название метода Беллмана.
Теорема 4.2.1
Траектория 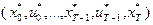 , построенная методом Беллмана, является оптимальной.
, построенная методом Беллмана, является оптимальной.
Доказательство. Траектория 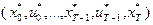 является допустимой, поскольку она удовлетворяет ограничениям задачи (4.2.1) и условию (4.2.2). По построению справедливы равенства:
является допустимой, поскольку она удовлетворяет ограничениям задачи (4.2.1) и условию (4.2.2). По построению справедливы равенства:
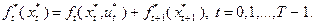
Сложим эти равенства:
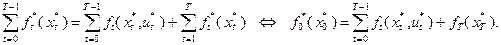 (4.2.5)
(4.2.5)
Здесь при записи последнего слагаемого учтено равенство (4.2.3). Полученное выражение по смыслу является значением целевой функции задачи (4.2.1). Рассмотрим некоторую произвольно выбранную допустимую траекторию 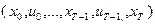 и покажем, что она не лучше траектории
и покажем, что она не лучше траектории 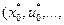
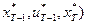 . Тем самым будет доказана оптимальность последней. Из соотношения (4.2.4) вытекает справедливость неравенств:
. Тем самым будет доказана оптимальность последней. Из соотношения (4.2.4) вытекает справедливость неравенств:
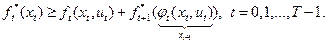
В результате сложения этих неравенств с учетом (4.2.3) получим:
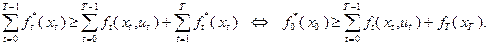
Поскольку 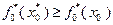 , из последнего неравенства и из (4.2.5) следует
, из последнего неравенства и из (4.2.5) следует
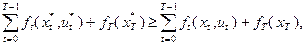
т.е. траектория 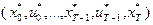 является оптимальной. Теорема доказана.
является оптимальной. Теорема доказана.
Следует отметить, что оптимальных траекторий может быть много. Это относится как к траекториям управлений системой, так и к траекториям ее состояния.
Дата добавления: 2021-05-28; просмотров: 432;











