РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА

Распределение Максвелла дает количественное распределение молекул по величине их скорости. Для описания этого распределения рассмотрим воображаемое пространство скоростей (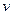 –пространство). По осям координат в таком пространстве откладываются составляющие скорости 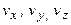. Скорости каждой молекулы в таком пространстве соответствует точка. Из-за столкновения молекул положения каждой из точек быстро изменяются с течением времени. Однако в равновесном состоянии плотность точек в каждом месте пространства с течением времени не изменяется.

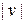Очевидно, что все направления движения равноправны, поэтому расположение точек относительно начала координат будет сферически симметричным. Это означает, что плотность точек может зависеть только от модуля скорости или от .

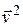Обозначим плотность точек произведением 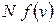, где 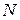– полное число молекул в данной массе газа, а 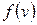– некоторая функция от модуля скорости.

Точки, изображающие молекулы со скоростями от 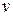до 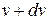, заключены в шаровом слое пространства скоростей между сферами с радиусам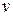и и 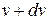. Объем этого слоя равен:

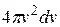. (9.01)

Следовательно, количество молекул со скоростями в указанном интервале

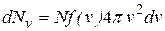. (9.02)

Разделив 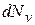на N, найдем вероятность того, что скорость произвольно взятой молекулы окажется в рассматриваемом интервале:

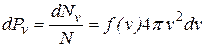. (9.03)

Таким образом, функция

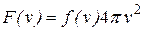(9.04)

играет роль функции распределения молекул по скоростям.

Вид этой функции был теоретически найден Максвеллом:

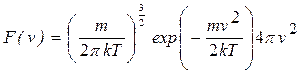(9.05)

Примечателен тот факт, что в показателе экспоненты в (9.05) стоит отношение кинетической энергии молекулы к величине kT, характеризующей среднюю энергию молекул газа. Примерный вид графика функции 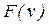показан на рисунке 9.2. При малых значениях скорости вид графика определяется множителем 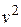. Однако с ростом скорости экспоненциальный множитель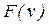 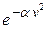в (9.05) убывает быстрее, чем растет 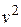(показательная функция «сильнее» степенной). Поэтому график функции 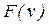достигает максимального значения, а затем уменьшается по закону, близкому к экспоненциальному.

Воспользовавшись функцией распределения молекул по скоростям Максвелла, найдем среднюю скорость молекул. По формуле (8.25) среднее значение случайной величины, фкункция распределения 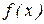которой известна, определяется соотношением:

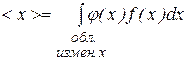. (8.25)

В наших обозначениях функцией распределения является 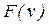. Положим 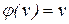. Скорость молекул намного меньше скорости света в пустоте, поэтому верхний предел интегрирования можно положить равным бесконечности. Тогда:

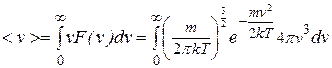. (9.06)

Выполнив интегрирование, получим:

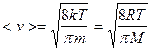(9.07)

Аналогичным образом можно найти среднюю квадратичную скорость:

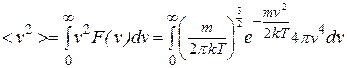. (9.08)

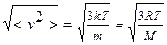(9.09)

Очевидно, что наиболее вероятной скоростью молекул является скорость, соответствующая максимуму функции распределения. Для ее вычисления найдем производную от 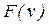по 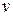и приравняем ее нулю:

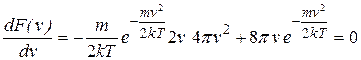(9.10)

Или, после вынесения общего множителя за скобки,

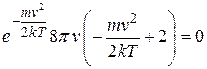. (9.11)

Значения 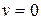и 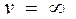удовлетворяют уравнению (9.11) , но они соответствуют минимумам 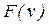. Следовательно, максимуму соответствует равенство нулю выражения в скобках, а значит

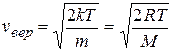. (9.12)

Представляет интерес рассмотреть, как изменяется 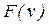при изменениях температуры. Для этого подставим значение скорости (9.12) в (9.5):

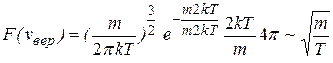. (9.13)

Таким образом, при повышении температуры максимум 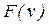смещается вправо ( 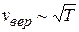) и становится меньше, как это показано на рисунке 9.3.

Важно иметь в виду, что при этом площадь под кривой остается постоянной, поскольку функция распределения обладает свойством

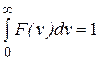(9.14)

Действительно, интеграл (9.14), в соответствии с определением функции распределения, дает вероятность обнаружения молекулы со скоростью от0до ∞, т.е. с какой-нибудь скоростью, а это вероятность достоверного события, всегда равная единице. Условие (9.14) называют условием нормировки функции распределения.

Отметим, что если рассматривать распределение по скоростям различных газов при фиксированной температуре, то переход к более легким молекулам отражается на графике функции распределения аналогично переходу к более высоким температурам.

Вычисления показывают, что при нормальных условиях у 70% молекул скорость отличается от 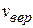не более, чем на 50%. Скоростью большей 3 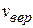обладают не более 0,04% молекул. Скорость более 5 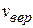встречается у одной молекулы из 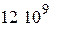молекул. Другими словами скорости, а значит и энергии, молекул действительно группируются вблизи наиболее вероятного значения, как мы говорили ранее.

Отметим, в заключении, что, произведя замену переменных в (9.5), можно получить распределение молекул по значениям кинетической энергии:

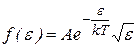, (9.15)

где 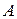- есть коэффициент пропорциональности (нормировочный коэффициент).