ДАВЛЕНИЕ ГАЗА НА СТЕНКУ В МКТ

В равновесном состоянии молекулы газа движутся хаотически: все направления движения равновероятны и ни одному из них не может быть отдано предпочтение перед другими. Величина скорости молекул вследствие их многочисленных столкновений может различаться довольно сильно. Однако как очень большие, так и очень малые значения маловероятны. Скорости большинства молекул группируются вблизи некоторого наиболее вероятного значении, близкого к среднему. (Более подробно о характере теплового движения молекул – самостоятельно).

Естественно предположить, что давление газа на стенки сосуда обусловлено большим количеством ударов отдельных молекул о стенку. Рассмотрим, как это предположение обосновывается в молекулярно кинетической теории (МКТ).

Для упрощения рассуждений предположим, молекулы в газе движутся вдоль трех взаимно перпендикулярных направлений, так что из 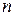молекул в единице объема 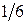часть летит по направлению к элемент 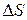стенки сосуда.

Выделим мысленно из 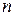молекул в единице объема те 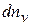молекул, скорости которых лежат в интервале от 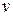до 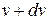. За время 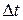до элемента 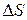долетят те молекулы из 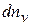, которые находятся в объеме цилиндра с основанием 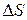и высотой 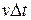, а их скорости направлены к 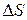. Следовательно, число ударов этих молекул

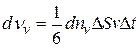. (8.1)

При соударении со стенкой каждая из молекул передает стенке импульс 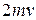, т.к. направление движения изменяется на противоположное. Следовательно, суммарный импульс, переданный элементу поверхности стенки сосуда 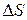за время 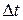молекулами со скоростями в интервале от 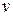до 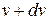будет равен:

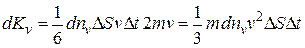. (8.2)

Общий импульс, получаемый элементом 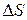стенки от молекул всех скоростей, за 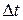, мы получим, сложив 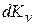для всех скоростей от 0 до 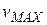(скорость молекул во всяком случае не превосходит скорость света в пустоте):

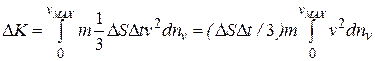. (8.3)

Интеграл в (8.3) можно найти, если учесть, что величина

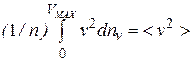(8.4)

есть, по определению, среднее значение квадрата скорости. Выразив из (8.4) интеграл и подставив его значение в (8.3), получим:

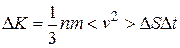(8.5)

Разделив (5) на 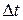, получим по второму закону Ньютона силу давления молекул на 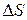, а разделив на 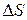, получим выражение для давления:

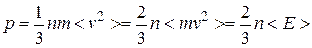(8.6)

где 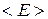- среднее значение кинетической энергии поступательного движения молекул.