Теорема об оценке двойного интеграла
Если функция f(x,y) непрерывна в области D и удовлетворяет неравенствам
m£f(x,y) £M , (x,y) ÎD,
то 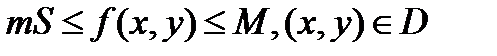 ,
,
где m и М – соответственно наименьшее и наибольшее значения
функции f(x,y) в замкнутой области D ;
S – площадь области D .
7. Теорема о среднем значении
Разделим все части неравенства
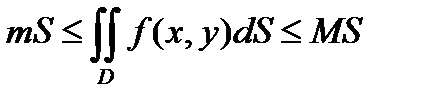 на S;
на S;
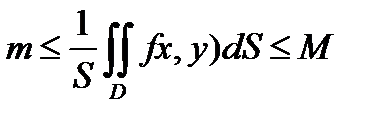 положим
положим 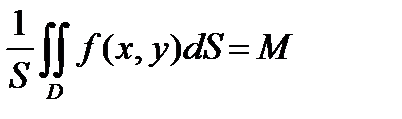 .
.
Тогда m£m£M .
По теореме о промежуточных значениях в области D найдётся такая точка (x, h), что f(x, h) = m :
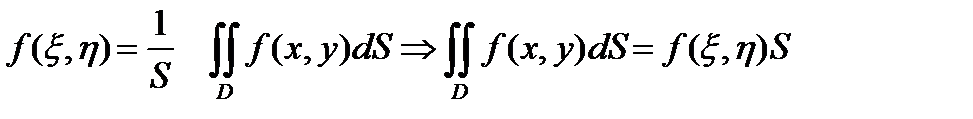 .
.
Последняя формула выражает собой теорему о среднем и показывает , что если функция f(х, у) непрерывна в замкнутой области D площади S , то в этой области найдётся такая точка (x, h) , что
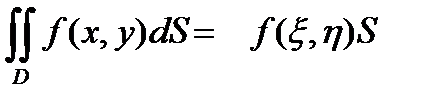 .
.
.Вычисление двойного интеграла в декартовой системе координат
Рассмотрим способ вычисления двойного интеграла путём его приведения к повторному (двукратному) интегралу , т.е. последовательному вычислению двух простых интегралов .
Мы ограничимся не вполне строгим , но зато простым геометрическим выводом, основанным на том , что двойной интеграл представляет объём цилиндричес-кого тела с основанием D , ограниченного сверху поверхностью z = f(x,y) .
В разделе " Определённый интеграл " мы уже имеем дело с задачей вычисления объёма тела по его поперечным сечениям .
Рассмотрим цилиндрическое тело , содержащееся между параллельными плоскостями х = а и х = b .
Допустим , что в сечении тела плоскостью , проведённой через точку х = х0 , х0Î[ a,b] , перпендикулярной оси Ох , получается фигура , имеющая площадь S(x0) ( причём S(x) – непрерывная функция , х Î[ a,b] ).
Тогда , как известно , объём V тела вычисляется по формуле
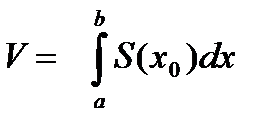 . (6.7.9.)
. (6.7.9.)
Пусть данное тело ограничено сверху поверхностью z = f(x,y) ³ 0 , с боков – цилиндрической поверхностью с образующими , параллельными оси Oz , снизу - плоской фигурой D на плоскости Оху ( область D – простая ).
Пусть y2 = у2(x) – уравнение ANB ;
у1 = у1(x) – уравнение AМB.
Криволинейная трапеция MPQN ограничена сверху линией z = f(x0,y), где уÎ[у1,y2] . Как известно , площадь криволинейной трапеции
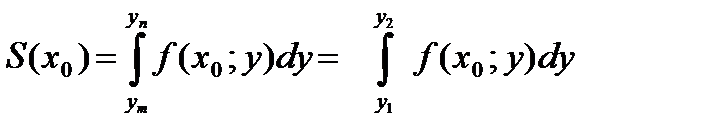 .
.
Поскольку сечение х = х0 было взято произвольно , то для любой точки хÎ[a,b] будем иметь
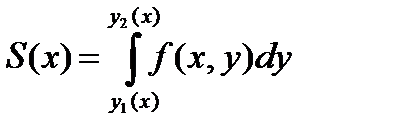 , (6.7.10)
, (6.7.10)
где уже пределы интегрирования у1(х) и у2(х) – переменные величины; они зависят от х.
Подставляя это значение в формулу ( 6.7.4 ) , получим
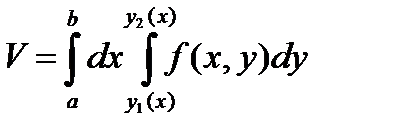 . (6.7.11)
. (6.7.11)
Выражение , стоящее в правой части формулы (6.7.12) , называется повторным (двукратным) интегралом функции f(x,y) по области D .
Но объём цилиндрического тела выражается двойным интегралом :
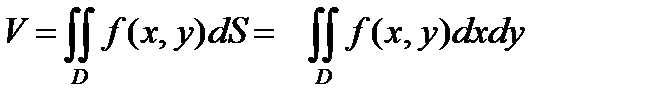 . (6.7.12)
. (6.7.12)
Сопоставляя равенства (6.7.11) и (6.7.12) , получаем формулу
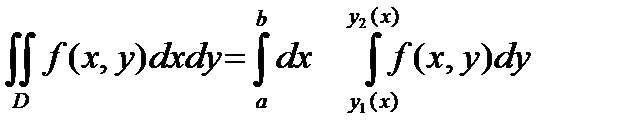 (6.7.13)
(6.7.13)
приводящую двойной интеграл к повторному , в котором интегрирование 1) сначала выполняется по у при произвольном , но постоянном х – внутреннее интегрирование , 2) а затем полученный результат интегрируется по х – внешнее интегрирование; при этом пределы внутреннего интеграла у1(х) и у2(х) – функции от х , а пределы внешнего интеграла - постоянные а и b .
Производя сечение цилиндрического тела плоскостями , параллельными плоскости Oxz , и рассуждая аналогичным образом , мы найдём , что
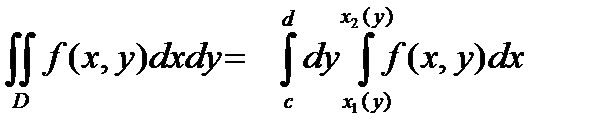 . (6.7.14)
. (6.7.14)
Здесь интегрирование сначала производится по переменной х при постоянном у , а затем полученный результат интегрируется по у ; при этом пределы внутреннего интеграла х1(у) и х2(у) – известные функции от у ( мы их находим из уравнений контура ) , заданные в промежутке [c,d] , а пределы внешнего интеграла – постоянные с и d , являющиеся ординатами крайних ( снизу и сверху соответственно точек контура z ( точек С и F) .
Сопоставляя формулы (6.7.13) и (6.7.14) , находим
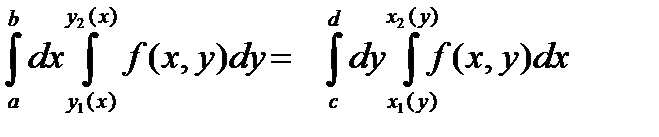 . (6.7.15)
. (6.7.15)
Последнее равенство показывает , что при перемене порядка интегрирования пределы внутреннего и внешнего интеграла изменяются ( в зависимости от формы контура z ) .
Значение формул и состоит в том , что они сводят вычисление двойного интеграла по области D к последовательному вычислению двух "обычных "("однократных") определённых интегралов от функции одной переменной ( методы вычисления таких интегралов уже ранее были изучены ) .
Какую из этих формул удобнее применить в том или ином случае , устанавливается в зависимости 1) от вида функции f(x,y) или от 2) вида области D .
Были установлены в предположении , что область D простая ( т.е. граница области D пересекается прямыми , параллельными как оси Ох , так и оси Оу , не более чем в 2 точках .)
В ряде случаев область D интегрирования не является простейшей областью , но может быть разбита на несколько простых областей , например , на D1,D2 ,D3 ( рис.1.7).
В этих случаях , пользуясь свойством 3 двойного интеграла , двойной интеграл по всей области D представится в виде суммы интегралов по этим областям и каждый из них вычисляется путём сведения к повторному интегралу .
Если область интегрирования представляет собой прямоугольник D : а £ х £b , c£y£d ( т.е. со сторонами , параллельными осям координат ) , то пределы как внешнего , так и внутреннего интеграла постоянны .
Доказано , для любого значения х , заключённого между а и b , переменная у меняется в пределах от с до d . Обратно , для любого у меняется в пределах между с и d, переменная х меняется в пределах от а и b .
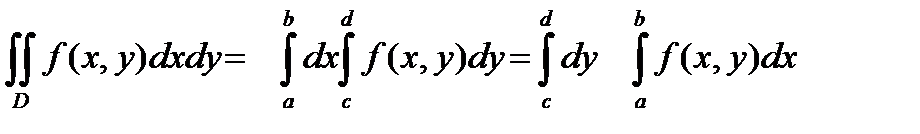
Следует твёрдо помнить , что в случае произвольной области интегрирования постоянны только пределы внешнего интеграла ; пределы же внутреннего интеграла переменны ( являются функциями переменной внешнего интеграла ) .
Практика показывает , что при вычислении двойных интегралов студент , как правило , испытывает трудности , связанные с расстановкой пределов интегрирования .
Рассмотрим ряд примеров
Пример 6.8.1.
Записать двойной интеграл 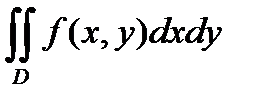 в виде повторных интегралов двумя способами , если область D ограничена прямой у = х2 .
в виде повторных интегралов двумя способами , если область D ограничена прямой у = х2 .
Решение
а. Сначала применим формулу (т.е. интегрируем сначала по у , считая х постоянным , а затем по х в пределах от а= 0 до b =1 , представляющих собой абсциссы крайних точек контура области ).
Чтобы найти пределы для у, поступают так : возьмём на оси Ох произвольную точку х между 0 и 1 и проведём через неё прямую , параллельную оси Оу , в направлении этой оси .
Точка входа этой прямой в области D лежит на параболе у = х2 , а точка выхода этой прямой из области D лежит на прямой у= х.
Уравнения этих линий дают нам соответственно нижний и верхний пределы внутреннего интеграла .
Таким образом имеем :
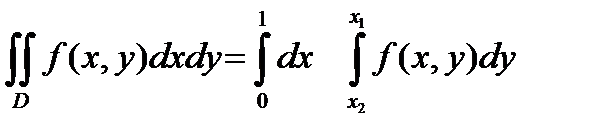 .
.
б. Применим теперь к двойному интегралу формулу (9).
В этом случае внутренний интеграл берётся по переменной х, считая у постоянным , а затем по у , уÎ[0,1] ( где 0 и 1 – наименьшая и наибольшая ординаты крайних этих точек контура области D) .
Чтобы установить , каковы будут пределы внутреннего интеграла по х , возьмём произвольную точку у на оси Оу в промежутке [0,1] и проведём через неё прямую . параллельную оси Ох , в направлении этой оси .
Так как точка входа этой прямой в области D лежит на прямой х = у , а точка выхода её из области D лежит на параболе 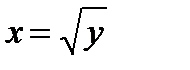 , то из уравнения этих линий дадут нам нижний и верхний пределы внутреннего интеграла .
, то из уравнения этих линий дадут нам нижний и верхний пределы внутреннего интеграла .
Следовательно имеем :
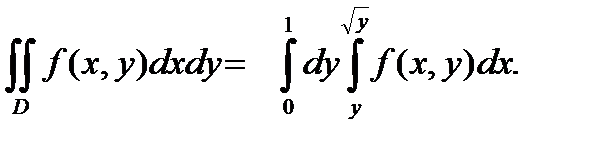
Пример 6.8.2.
Вычислить 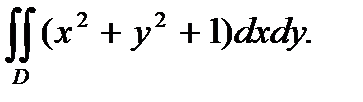
Область D :- 1 £ х £ 1 , 0 £ у £ 2 ( т.е. задана такими неравенствами)
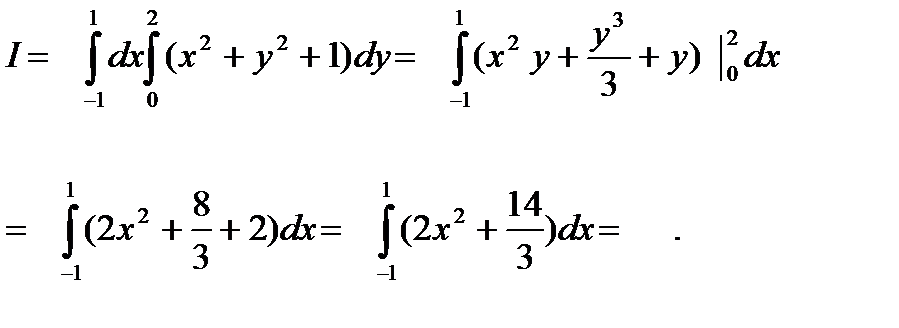
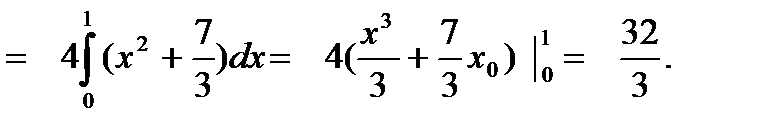
Пример 6.8.3.
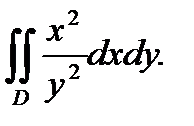 = ? Область D : у = х , х = 2 , ху = 1.
= ? Область D : у = х , х = 2 , ху = 1.
Решение
При +1 £х£ 2 у изменяется от у = 1/х до у= х .
Пределы внешнего интеграла по переменной х : это будет абсциссы самых левых и самых правых точек области D .
Чтобы установить пределы внутреннего интеграла по у , возьмём произвольную точку х между 1и 2 на оси Ох и проведём через неё прямую , параллельную оси Оу . Точка входа этой прямой в область D лежит на гиперболе у = 1/х , а точка выхода на прямой у = х . Уравнения этих линий дают нам соответственно нижний и верхний пределы внутреннего интеграла .
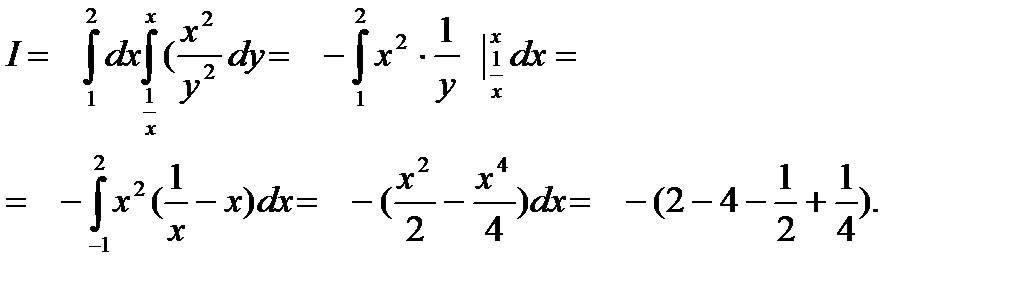
Дата добавления: 2016-06-05; просмотров: 6765;











