Изменение порядка интегрирования в двойном интеграле
Если область D является простой , то для вычисления двойного интеграла применимы обе формулы (1.5) и (1.6) .Следовательно :
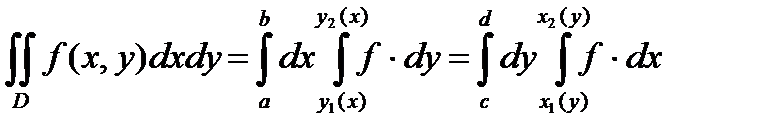 .
.
Это равенство показывает , что повторное интегрирование не зависит от порядка интегрирования .
Этим обстоятельством часто пользуются при вычислении двойных интегралов , выбирая ту из двух формул , которая приводит к более простым выкладкам .
Пример 6.8.4.
Изменить порядок интегрирования в следующем интеграле :
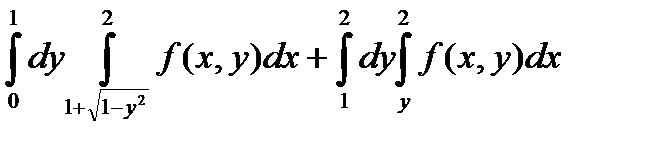 .
.
Решение
Область интегрирования непосредственно не дана . Мы должны выяснить её вид по пределам повторных интегралов .Итак , по пределам повторных интегралов восстановим область D интегрирования .
Так как внутренний интеграл берётся по х , то пределы внутреннего интеграла показывают , какими линиями область D ограничена слева и справа .
Уравнения этих линий : 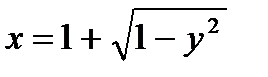 Û (х –1)2 + у2 = 1; х =2 ; х= у
Û (х –1)2 + у2 = 1; х =2 ; х= у
Приступим к изменению порядка интегрирования :
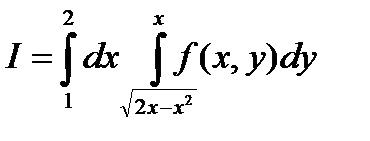
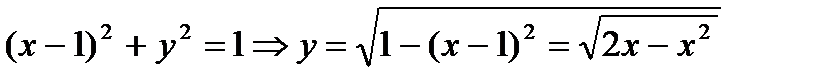
Этот пример показывает , как важно с самого начала продумать порядок интегрирования , т.е. предварительно следует посмотреть , для какой переменной лучше выбрать постоянные пределы интегрирования и выбрать тот способ . при котором двойной интеграл будет представлен меньшим числом повторного интеграла .
Пример 6.8.4. – Изменить порядок интегрирования в интеграле 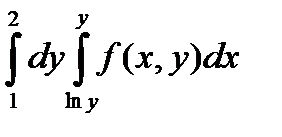
y =ex ,
y = 2 ,Ûex = 2 Þx = ln 2 .
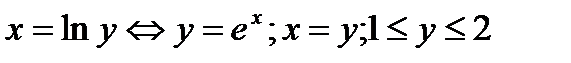
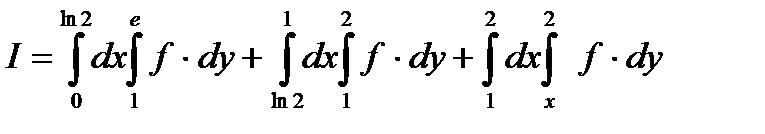
Пример 6.8.5.Вычислить 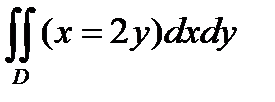 по области D , ограниченной линиями :
по области D , ограниченной линиями : 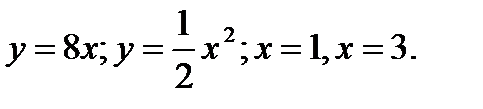
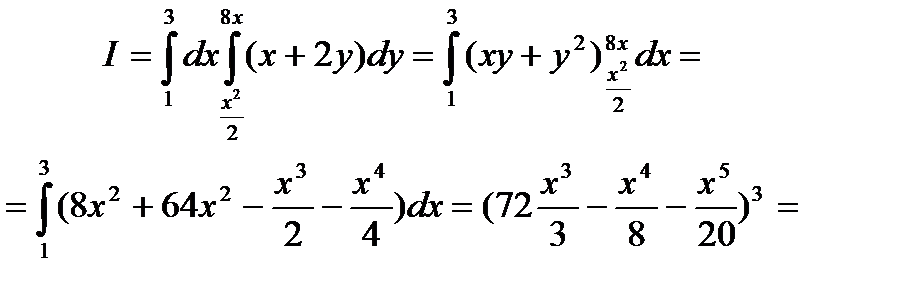
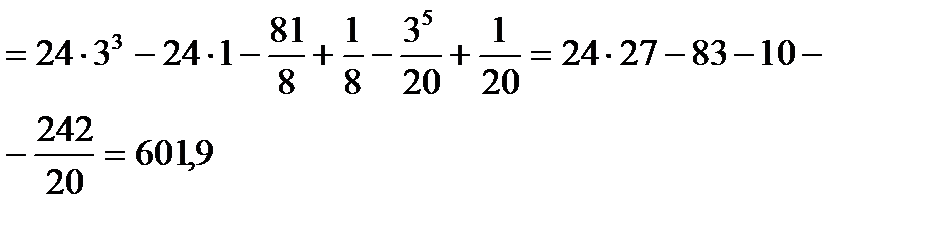
Дата добавления: 2016-06-05; просмотров: 18774;











