Вычисление объемов тел
Вычисление объема тела по площади поперечногo сечения
Пусть дано тело произвольной формы, заключенное между плоскостями x=a и x=b. Кроме того, пусть известна площадь любого поперечного сечения (т.е. площадь сечения, образованного плоскостью перпендикулярной к оси ОХ - тела). Требуется вычислить объем этого тела.
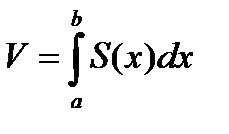 , где S – площадь поперечного сечения.
, где S – площадь поперечного сечения.
Объем тела вращения
Пусть вокруг оси ОХ вращается криволинейная трапеция, ограниченная осью ОX, прямыми x=a и x=b и кривой 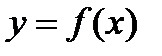 , где
, где 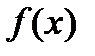 - непрерывная, неотрицательная на отрезке [a; b] функция. Тогда эта криволинейная трапеция опишет тело, являющееся телом вращения.
- непрерывная, неотрицательная на отрезке [a; b] функция. Тогда эта криволинейная трапеция опишет тело, являющееся телом вращения.
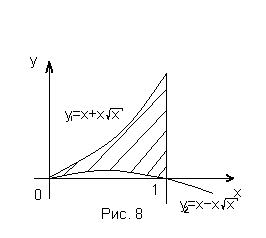
Пример 6. 7.7.Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной двумя ветвями кривой 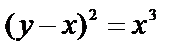 и прямой х=1.
и прямой х=1.
Решение:
искомый объем получается как разность двух объемов, получающихся при вращении вокруг оси ОХ двух криволинейных трапеций, ограниченных сверху соответственно кривыми 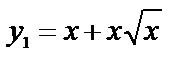 и
и 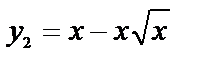 . Область определения функции
. Область определения функции
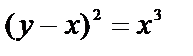
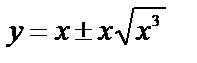
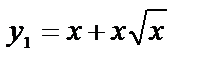
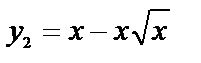
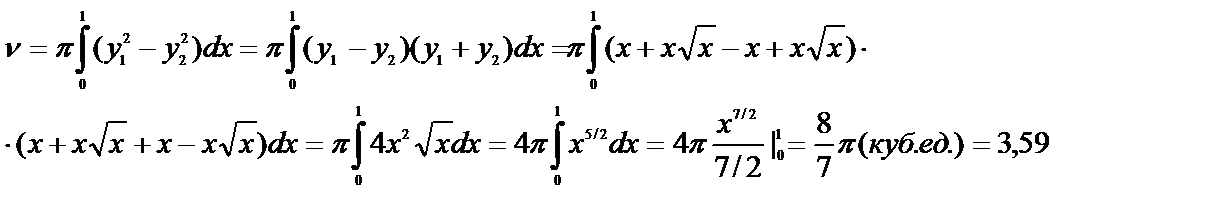
Вычисление длины дуги
Длина дуги в полярных координатах
Пусть на плоскости XOY дана кривая, уравнение которой y=f(x), где f(x) – непрерывная на отрезке [a, b] функция.
Пусть производная 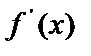 этой функции также непрерывная функция на отрезке [a,b].
этой функции также непрерывная функция на отрезке [a,b].
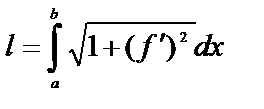 .
.
Пример 6.7.7..Вычислить длину дуги кривой 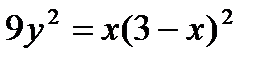 между точками пересечения ее с осью ОХ.
между точками пересечения ее с осью ОХ.
Решение:
у=0, 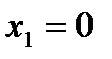 ,
, 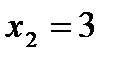 .
.
Т.к. ув четной степени, то кривая симметрична относительно оси ОХ.
ОДЗ: 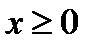 .
.
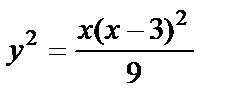 ,
, 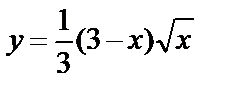
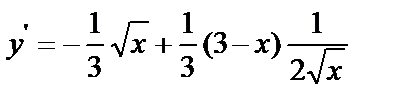 :
: 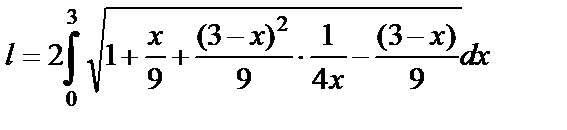
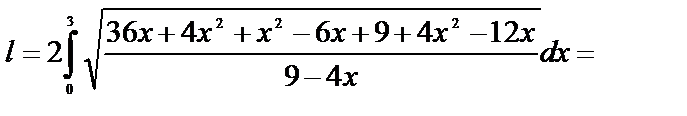
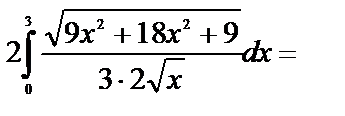
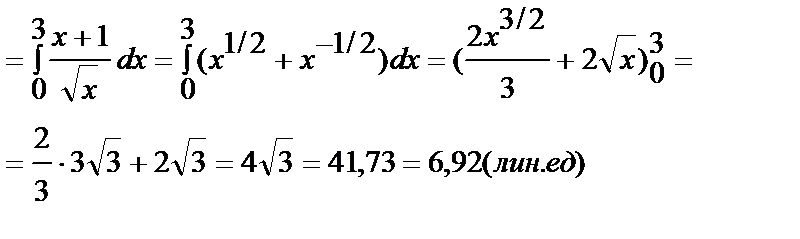
Длина дуги кривой, заданной параметрическими уравнениями 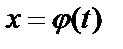 ,
, 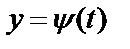 , где
, где 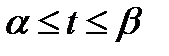
Пусть функции 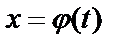 ,
, 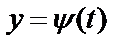 - непрерывные на
- непрерывные на 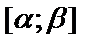 функции, с непрерывными производными
функции, с непрерывными производными 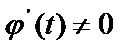 ;
; 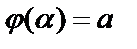 ,
, 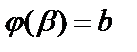 .
.
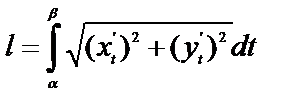 .
.
Пример 6.7.8. Вычислим длину траектории
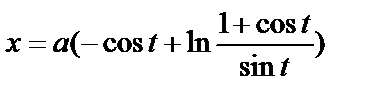 ,
, 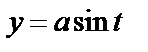 от
от 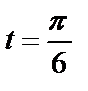 до
до 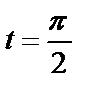 .
.
Решение:
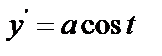 ;
; 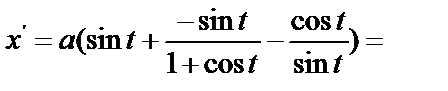
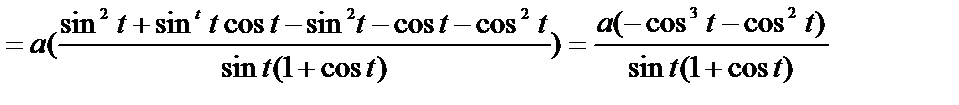
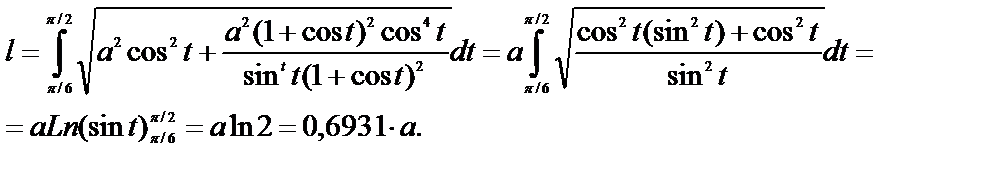
Длина дуги в полярных координатах
Пусть в полярной системе координат дана кривая, уравнение которой 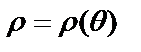 , где
, где 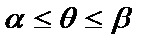 . Функция
. Функция 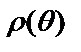 имеет непрерывную производную на сегменте
имеет непрерывную производную на сегменте 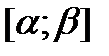
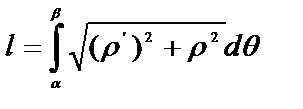 .
.
Пример 6.7.9.Найти всю длину кривой 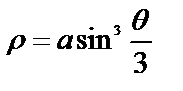 .
.
Решение: 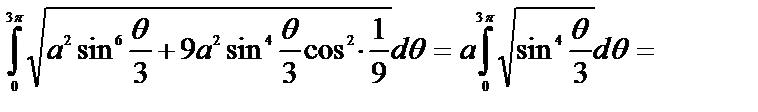
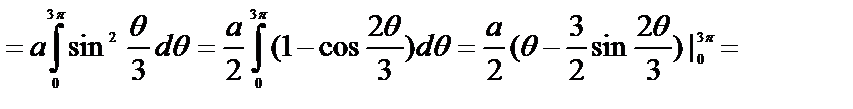
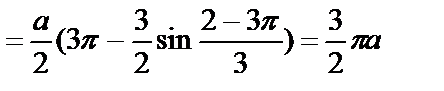 .
.
Здесь имеем 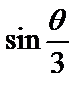 при
при 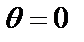 и при
и при 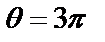 .
.
Дата добавления: 2016-06-05; просмотров: 3291;











