Алгоритм обработки РН при оценке СлСПИ.

1. Исключить известные СиСПИ;

2. Найти среднее значение (оценку математического ожидания) – результат измерения (РИ)

a_i = A + D_I 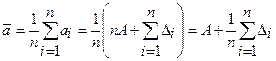При n®¥ сумма случайных

погрешностей стремится к нулю, поэтому 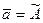- оценка результата измерения.

3. Вычислить оценку СКО РН:

а) v_i = a_i - ;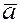

б) 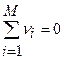, если не равно 0, то нужно проверить верность выполнения п. 2;

в) 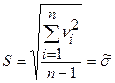- оценка среднеквадратичного отклонения;

Распределение Стьюдента:

Нормальный закон пригоден для большого числа наблюдений, а как быть, когда число наблюдений мало? Прибегают к распределению Стьюдента :

,

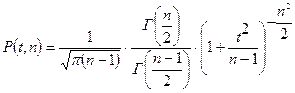где Г – гамма-функция,

n – число наблюдений,

t – нормированная случайная погрешность среднего значения:

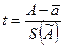
A – истинное значение,

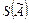- оценка среднеквадратичного отклонения РИ.

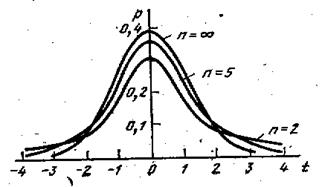
Из графиков распределения Стьюдента видно, что при n®¥оно совпадает с нормальным.

4. Вычислить оценку СКО РИ:

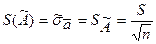
Формула показывает, что с увеличением количества опытов погрешность РИ падает, и при n ® ¥, случайная погрешность РИ стремиться к 0, а сам РИ, следовательно, к истинному значению, т.е. 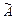® A.

5. Проверка гипотезы о принадлежности к нормальному распределению;

а) n < 15 – невозможно определить;

б) 15 ³ n ³ 50 – определение по составному критерию ГОСТ 8.207-76;

в) n > 50 – определение по ГОСТ 11.06-74;

6. Выявление грубых погрешностей осуществляют в соответствии с ГОСТ 11.002-73, если есть анормальный результат наблюдения – его нужно исключить из ряда наблюдений и повторить вычисления с п. 2.;

7. Определить интервальные оценки СлСПИ:

а) задан доверительный интервал СлСПИ, Е – граница доверительного интервала. Вычисляют коэффициент Стьюдента t_a

,

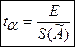значения P определяется по таблице распределения Стьюдента,

б) задана доверительная вероятность – P. С помощью таблицы распределения Стьюдента по известным P и n находят t_a, а затем

E = t_a × 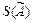доверительный интервал СлСПРИ;

8. Оформить результат измерения в соответствии с МИ 1317-86.