Определение двойного интеграла

Пусть дана функция z = f(x,y) , определённая и непрерывная в некоторой замкнутой области D , граница Г которой простая замкнутая линия ( такую замкнутую область называют простой областью ).

Разобьём область D на n частичных (элементарных) областей (простых ) D_i ( i=1,2,... ,n) ( без общих внутренних точек ) с помощью некоторой сети кривых .

Площади этих областей обозначим соответственно через DS₁, DS₂, . . . , DS_n .В пределах каждой частичной области D_i выберем произвольным

образом по точке (x_i ;h_i) и составим сумму :

.

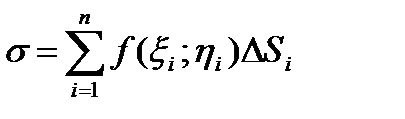Всякую такую сумму называют интегральной суммой для функции f(x,y) соответственной области D .

Меняя сеть разбиения и способ выбора точек в частичных областях , мы можем составить бесконечно много интегральных сумм , различных между собой.

Будем теперь неограниченно увеличивать число n разбиений области D на частичные области D_i , но так , чтобы все d(D_i) взятых областей стремились к нулю при этом .

Может случится , что тогда интегральная сумма s будет иметь предел , не зависящий ни от способа разбиения области D на частные области D_i ; ни от способа выбора точек (x_i ; h_i) в этих областях.

Этот предел I записывают следующим образом :

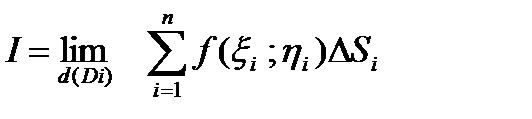. (6.7.7)

Определение 1

Если при d(D_i) ® 0 интегральная сумма s имеет предел , то этот предел называется двойным интегралом от функции f(x,y) , взятым по области D , и обозначается

.

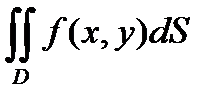Функция f(x ,y) при этом называется интегрируемой в области D .

Следовательно , по определению

.

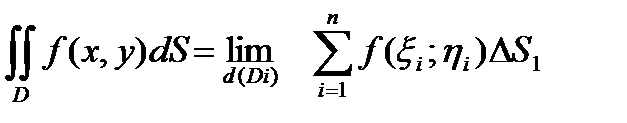Символ dS называется элементом площади .

Возвращаясь к рассмотренной выше задаче , можно , исходя из приведённого определения , сказать , что в случае интегрируемости в D функции f(x,y) объём цилиндрического тела равен двойному интегралу от функции f(x,y) по области D :

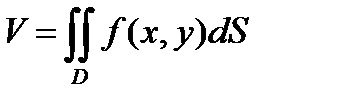. (6.7.8)

Эта формула показывает , что двойной интеграл от неотрицательной непрерывной функции геометрически выражает собой объём цилиндрического тела .

Элемент площади dS = dxdy , т.е. равняется произведению дифференциалов независимых переменных .

Доказано , если разбивать область D прямыми , параллельными осям ОХ и ОУ , то частичными будут служить прямоугольники .

Площадь каждой частичной области DS будет равна произведению DхDу.

Поэтому элемент площади dS = dxdy .

Таким образом òò является прямым обобщением понятия простого определения ò на случай функции двух переменных .