Шлакование топлива. Стационарное отравление самарием
Схема отравления реактора 149Sm показана на рис. :
| 0,013 -b -b 235U + n ¾®149Nd ¾®149Pm ¾®149Sm + n ¾®150Sm (шлак) 2 ч 53,1 ч |
Рис. Схема отравления реактора 149Sm
Из рис. видно, что образование 149Sm происходит в результате цепочкиb- - распадов ядер неодима 149Nd и прометия 149Pm (с удельным выходом gNd=gPm=0,013). Выгорание 149Nd и 149Pm в цепочке не учитывается, так как оба эти нуклида имеют сравнительно малые сечения радиационного захвата. Микроскопическое сечение поглощения тепловых нейтронов 149Sm sa,Sm»5´104 б. Убыль конценрации 149Sm происходит вследствие его выгорания с образованием 150Sm.
При составлении уравнений кинетики отравления топлива самарием вводят допущение о том, что 149Pm образуется непосредственно как продукт деления 235U. Правомерность этой предпосылки обусловлена тем, что период полураспада 149Nd намного меньше периода полураспада 149Pm. С учетом введенного допущения кинетика отравления топлива может быть описана двумя дифференциальными уравнениями (для 149Pm и для 149Sm), каждое из которых является частным случаем зависимости (9.13).
Так как концентрация 149Pm убывает только из-за его распада со скоростью lPmNPm и в результате с такой же скоростью увеличивается концентрация 149Sm, а скорость убыли концентрации 149Sm определяется практически только скоростью реакции захвата тепловых нейтронов, с учетом принятых допущений уравнение отравления самарием ядерного топлива будут иметь вид:
| dNPm/dt = gPmsf5N5j - lPmNPm | (8.20) |
| dNSm/dt = lPmNPm - sa,SmNSmj | (8.21) |
Здесь lPm = 0,357´10-5 с-1 - постоянная распада 149Pm.
Состояние работающего реактора, при которм концентрация 149Sm не изменяется во времени, называется стационарным отравлением самарием (на практике это понятие часто отождествляется с потерей реактивности при достижении равновесной концентрации 149Sm в работающем реакторе). Из (10.16) следует, что такое состояние наступает при равенстве скоростей образования и убыли самария.
Как и для ксенона, условие стационарности для самария может быть сформулированно в виде:
| dNSm/dt = dNPm/dt = 0. | (8.22) |
Используя (8.17), из (8.21) и (8.22) можно получить выражения, определяющие стационарные концентрации самария и прометия:
| NPmст = (gPmsf5N5/lPm) Ф = (gPmsf5Nu/lPm) zФ | (8.23) |
| NSmст = lPm NPmст/sa,SmФ = (gPmsf5Nu/sa,Sm)z | (8.24) |
Таким образом (как и для ксенона), равновесная концентрация 149Pm пропорциональна обогащению урана и плотности потока нейтронов. Стационарная концентрация 149Sm от плотности потока нейтронов не зависит, а определяется только обогащением урана. В этом - одно из принципиальных отличий стационарного отравления самарием от стационарного отравления ксеноном.
Переход от концентрации 149Sm к потере реактивности на отравление топлива самарием определяется выражением:
| rSm = - (sa,SmNSm/sa5N5) Qнотр | (8.25) |
В частном случае - для равновесной концентрации 149Sm - величина rSmст определяется посредством подстановки выражения для NSmст из (8.24) в (8.25) после замены в (10.18) Nuz на N5:
| rSmст = - (sf5/sa5) gPmQнотр | (8.26) |
Таким образом, потеря реактивности на стационарное отравление самарием зависит только от коэффициента использования тепловых нейтронов в неотравленной активной зоне, а значениеQнотр в свою очередь определяется обогащением ядерного топлива и не зависит от Ф.
Динамика достижения равновесных концентраций 149Pm и 149Sm характеризуется решением уравнений (8.20) и (8.21). При условии, что в момент t=0 NPm=NSm=0 и что после пуска реактора плотность потока нейтронов и концентрация 235U не изменяется, будем иметь:
| NPm(t)= NPmст(1 - exp(- lPmt); | (8.27) |
| NSm(t)=NSmст(1+lPmexp(-sa,SmФt)/(sa,SmФ-lPm)-sa,SmФexp(-lPmt)/(sa,SmФ-lPm)) | (8.28) |
Следовательно концентрация 149Pm при работе реактора на постоянной мощности увеличивается от исходного нулевого значения до NPmст по экспоненциальному закону. Так как точно стационарное значение NPm может быть достигнуто через бесконечно большой промежуток времени, примем за равновесную концентрацию прометия NPm= 0,95 NPmст, а время достижения этой концентрации будем считать временем установления процесса tустPm. Согласно этому условию и равенству (10.21) можем записать: NPm(tустPm)/ NPmст = 0,95 = 1 - exp(- lPm tустPm), откуда следует tустPm = ln 20/lPm» 10 сут.
В отличие от NPm(t) зависимость NSm(t) нельзя назвать чисто экспоненциальной, так как она определяется алгебраической суммой двух экспонент (10.22).
На рис. представленны графические зависимости NPm(t) и Nsm(t).
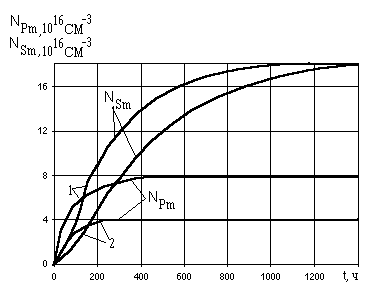
Рис.8.7. Изменение концентрации 149Pm и 149Sm в работающем реакторе: 1-при Ф=1014нейтр/(см2*с); 2 - при Ф=5*1013йтр/(см2*с)
Как видно из сопоставления кривых, с увеличением плотности потока нейтронов равновесная концентрация прометия увеличивается, а время ее достижения остается неизменным. Время же стабилизации NSm с увеличением Ф уменьшается, хотя сама величина NSmст при этом не меняется.
Скорость достижения стационарного отравления самарием, как это следует из рис. выше, существенно зависит от мощности ядерного реактора. Для Ф<1014 нейтр/(см2´с) tустSm, с приемлемой для практических приложений точностью, определяется выражением:
| tустSm = 2,2´1015/Ф | (8.29) |
При Ф>1014 нейтр/(см2´с) использование формулы (8.29) неправомерно, так как при этом время достижения равновесной концентрации 149Sm получается менее 10 суток, что меньше tустPm.
До сих пор все динамические аспекты отравления самарием расматривались при условии постоянства концентрации 235U и плотности потока нейтронов. Более реальным условием является постоянство мощности реактора с учетом выгорания топлива.
Теоритическим путем зависимость rSm(t) при Wp=const может быть получена посредством совместного решения уравнений (8.20), (8.21), (8.25), а также уравнения определяющего кинетику выгорания топлива при постоянной мощности реактора.
В заключение обратим внимание, что для ВВЭР потеря реактивности на стационарное отравление самарием по абсолютному значению примерно в 5 раз меньше потери реактивности на стационарное отравление ксеноном, а время достижения стационарного отравления самарием в 15-20 раз больше времени, стационарного отравления ксеноном.
Дата добавления: 2021-05-28; просмотров: 764;











