Нестационарное уравнение Шредингера.

Уравнения Ньютона в классической механике позволяют для макроскопических тел решить основную задачу механики – по заданным силам, действующим на тело (или систему тел), и начальным условиям найти для любого момента времени координаты тела и его скорость, т.е. описать движение тела в пространстве и времени.

При постановке аналогичной задачи в квантовой механике необходимо учитывать ограничения на возможность применения к микрочастицам классических понятий координат и импульса. Поскольку состояние микрочастицы в пространстве в данный момент времени задается волновой функцией, а точнее 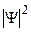- вероятностью нахождения частицы в точке x,y,z в момент t , основное уравнение квантовой механики является уравнением относительно пси-функции .

Это уравнение было получено в 1926 г. Шредингером. Как и уравнения движения Ньютона, уравнение Шредингера постулируется, а не выводится. Справедливость этого уравнения доказывается тем, что полученные с его помощью выводы находятся в хорошем согласии с экспериментами.

Уравнение Шредингера имеет вид

, (*)

здесь m – масса частицы, i – мнимая единица, - оператор Лапласа, результат действия которого на некоторую функцию

.

U(x,y,z,t) – в рамках наших задач потенциальная энергия частицы, движущейся в силовом поле. Из уравнения Шредингера следует, что вид пси-функции определяется функцией U, т.е. в конечном счете, характером сил, действующих на частицу.

Уравнение Шредингера дополняется важными условиями, которые накладываются на пси-функцию. Этих условий три:

1) функция ψ должна быть конечной, непрерывной и однозначной;

2) производные должны быть непрерывны

3) функция 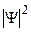должна быть интегрируема, т.е. интеграл должен быть конечным. В простейших случаях третье условие сводится к условию нормировки

Это означает, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице. Первые два условия – обычные требования, накладываемые на искомое решение дифференциального уравнения.