Нестационарное отравление самарием
После остановки ядерного реактора нарушается динамическое равновесие между скоростью появления 149Sm из 149Pm и скоростью его убыли из-за поглощения нейтронов. Убыль 149Sm прекращается, так как поток нейтронов практически равен нулю, а прибыль его из 149Pm продолжается до полного распада последнего с (Т1/2)Pm=53 ч. Практически через 8-10 сут распадается примерно 90%149Pm.
Процессы отравления реактора, после его остановки, ксеноном и самарием принципиально отличаются друг от друга. Ксенон как короткоживущий нуклид в конечном счете полностью распадается, а самарий, будучи стабильным, накапливается в активной зоне, причем увеличение его концентрации происходит до тех пор, пока не распадется весь 149Pm. Рост концентрации 149Sm влечет за собой снижение запаса реактивности. В теории реакторов этот процесс уменьшения запаса реактивности после остановки реактора, происходящий в результате распада накопившегося 149Pm с переходом его в 149Sm, называют прометиевым провалом.
Кинетика отравления топлива самарием после остановки реактора описывается уравнениями (8.21) и (8.22), которые в данном случае (j=0) принимают вид:
| dNPm/dt = - lPmNPm; | (8.30) |
| dNSm/dt = lPmNPm. | (8.31) |
Характер изменения концентраций 149Pm и 149Sm определяется решением уравнений (8.30) и (8.31). В результате интегрирования этих зависимостей при условии, что на момент остановки реактора (t=0) концентрации прометия и самария составляют NPm(0) и NSm(0), получим
| NPm = NPm(0)exp(-lPmt); | (8.32) |
| NSm = NSm(0) + NPm(0)(1 - exp(-lPmt)). | (8.33) |
Отсюда следует, что концентрации 149Pm и 149Sm после остановки реактора изменяются по экспоненциальному закону. Аналогичным образом изменяется и запас реактивности. Для иллюстрации сказанного на рис. представлены графические зависимости NPm(t), NSm(t) и rSm(t).
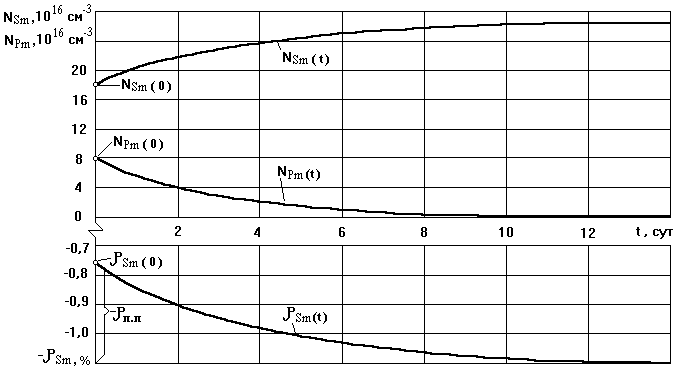
Рис.8.8. Изменение NSm, NPm, и rSm после остановки реактора, достигшего стационарного шлакования топлива при Ф=1014 нейтр/(см2*с)
Рассмотрен случай, когда на момент останова реактора было достигнуто стационарное отравление реактора самарием.
В разделе 10.1.2 было показано, что стационарное отравление ядерного реактора самарием не зависит от плотности потока нейтронов. Что же касается прометиевого провала, то его глубина:
| rп.п. = rSm(¥) - rSm(0), | (8.34) |
где rSm(¥) - потеря реактивности на отравление самарием при бесконечно длительной стоянке.
rSm(¥) является функцией j, поскольку чем больше j перед остановом реактора, тем больше при прочих равных условиях значение Npm(0).
Если на момент останова была достигнута равновесная концентрация 149Sm, то равенство (8.33) можно представить в виде:
| NSm = NSmст + (gPmsf5NuzФ/lPm)(1 - exp(-lPmt)); | (8.35) |
После подстановки (35) в (26) потеря реактивности на отравление самарием определиться выражением:
| rSm = rSmст + (gPmsf5sa,SmQнотрФ/(lPm sa5))(1 - exp(-lPmt)); | (8.36) |
Так как полная глубина прометиевого провала достигается при t=¥, в соответствии с (8.36) будем иметь:
| rп.п. = - gPmsf5sa,SmQнотрФ/(lPm sa5) | (8.37) |
Время достижения полной глубины прометиевого провала tустп.п.»10 сут. (получили аналогично tустPm).
Если перед остановкой реактор работал на номинальной мощности в течении времени, достаточного для получения равновесной концентрации 149Pm, и после останова бездействовал до тех пор пока не распался весь накопившийся плутоний, то потеря реактивности будет равна номинальной глубине прометиевого провала. Для каждого конкретного реактора по (8.37) может быть вычислена эта максимальная глубина прометиевого провала rп.п.ном.
Если перед остановкой реактор работал мало (NPmст не достигнуто), или мощность была не номинальной, или время стоянки (tст) было не достаточно для распада всего накопившегося прометия, то потеря реактивности rSm(tст) может быть определена в долях rп.п.ном.
Для удобства учета перечисленных факторов предлагается номограмма, представленная на рис. 10.11. В основу построения номограммы положенны следующие соображения:
а) если средняя мощность Wрср за рассматриваемый период работы реактора меньше номинальной, а время работы и время стоянки достаточны для достижения равновесной концентрации 149Pm и его полного распада после остановки реактора, то в соответствии с (8.37):
| rSm(tст) = (Wрср/ Wрном) rп.п.ном; | (8.38) |
б) если кроме отличия Wрср от Wрном недостаточны время работы t и время стоянки tст, то учет этих факторов осуществляется введением в (10.38) двух корректирующих сомножителей:
| rSm(tст) = (Wрср/ Wрном)(1 - exp(-lPmt))(1 - exp(-lPmtст))rп.п.ном | (8.39) |
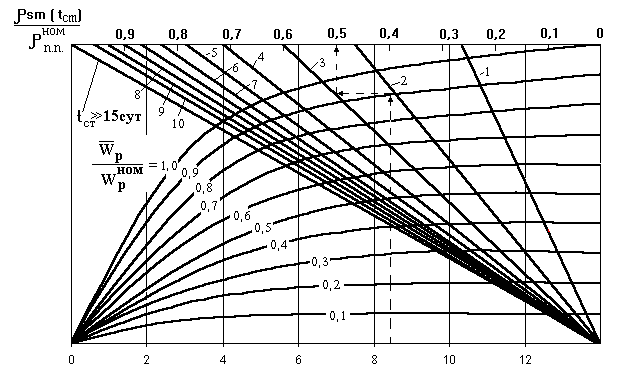
Рис.8.9. Номограмма для расчета нестационарного шлакования самарием
Семейство кривых на номограмме представляет собой графическую реализацию зависимости (Wрср/Wрном)(1-exp(-lPmt)), а семейство прямых определяет функцию 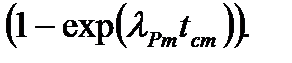 Штриховой линией показан пример использования номограммы при t=7 сут., Wрср=0,9 Wрном и tст=4 сут. Для получения искомого результата rSm(tст) остается умножить снятое с номограммы значение rSm(tст)/rп.п.ном на номинальную глубину прометиевого провала данного реактора.
Штриховой линией показан пример использования номограммы при t=7 сут., Wрср=0,9 Wрном и tст=4 сут. Для получения искомого результата rSm(tст) остается умножить снятое с номограммы значение rSm(tст)/rп.п.ном на номинальную глубину прометиевого провала данного реактора.
Если rSm(tст) по абсолютному значению будет превышать rXeст, то в конце компании, когда оперативный запас реактивности мал, может возникнуть угроза запирания реактора или, как еще говорят, может наступить “самариевая смерть“, заключающаяся в невозможности пуска реактора без перегрузки активной зоны. Запирание реактора возможно только при очень больших плотностях потока нейтронов. Для ВВЭР реальная угроза запирания практически отсутствует.
В ядерных реакторах на природном или слабообогащенном уране, где заметную роль играет накопление Pu из 238U, после остановки ядерного реактора продолжается накопление Pu из накопившегося во время работы ядерного реактора Np. В некоторых случаях по воздействию на реактивность этот положительный эффект сравним с отрицательным эффектом прометиевого провала и может его частично или полностью скомпенсировать.
ЧАСТЬ 9. РЕГУЛИРОВАНИЕ ЯДЕРНЫХ РЕАКТОРОВ
9.1. Общие подходы к управлению цепной реакцией деления в ядерном реакторе
9.2. Органы регулирования ядерных реакторов, их положение и эффективность
9.3. Борное регулирование
9.4. Выгорающие поглотители и их размещение
9.5. Нейтронно-физические измерения. Общая методика определения критической загрузки по кривым обратного счета
9.6. Методы градуировки органов управления системы управления и защит (ОР СУЗ) реактора, краткий обзор и их характеристика
9.7. Общая методика построения интегральной и дифференциальной характеристик поглощающего стержня
9.8. Общая методика определения мощностного и температурного эффектов и коэффициентов реактивности
9.9. Общая методика определения отравления реактора ксеноном
9.10. Аварийные режимы работы ядерных реакторов
Дата добавления: 2021-05-28; просмотров: 896;











