МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Понятие производной функции и понятие дифференциала функции являются одними из основных понятий математического анализа. Производная характеризует быстроту изменения функции при изменении её аргумента и может быть использована при математическом описании динамики химических реакций, при нахождении градиентов скорости, давления, концентрации, температуры и других величин.

Цель занятия:

· Уметь объяснить физический смысл производной первого и второго порядков.

· Научиться находить производные от элементарных и сложных функций.

· Научиться находить производные высших порядков.

· Научиться находить дифференциалы функций.

· Научиться приближенно вычислять функции с помощью дифференциала.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть на интервале ]а,в[ определена функция у=f(x). При приращении аргумента Dх функция получит приращение Df, которое определится равенством: Df=f(x+Dx)-f(x), тогда отношение:

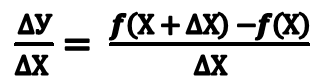
выражает среднюю скорость изменения функции f(x) относительно аргумента х на интервале ]х, х+Dх[.

Предел отношения приращения функции к приращению аргумента, когда Dх®0, при условии, что этот предел существует, называется производной функции в точке хÎ]а,в[:

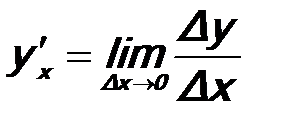
МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Решение задачи о нахождении скорости различных процессов приводит к понятию производной функции. Рассмотрим скорость прямолинейного движения. Пусть тело, двигаясь с переменной скоростью, прошло путь S, тогда средняя скорость равна:

,

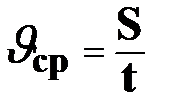где t- время движения тела. Разобьем весь путь на n отдельных участков:DS₁, DS₂,…,DS_n, пройденные соответственно за время: Dt₁, Dt₂,..,Dt_n, тогда скорости на этих участках:

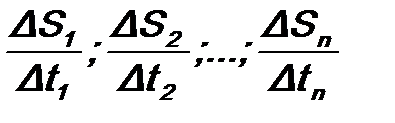
Если величину участков уменьшить, т.е. задать Dt®0, то средняя скорость стремится к пределу, который представляет собой скорость движения тела в данный момент времени или мгновенную скорость:

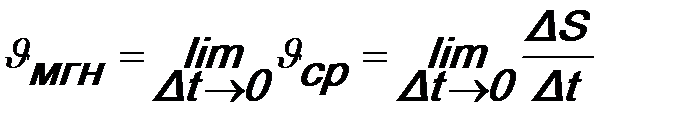
Таким образом, мгновенная скорость есть предел отношения приращения пути к приращению времени, когда приращение времени стремится к нулю.

1. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Пусть функция у=f(x) задана графически. Возьмем на кривой произвольно точку М(х,у). Зададим приращение аргументу Dх, тогда функция получит приращение Dу и на графике мы получим точку М₁ с координатами (х+Dх;у+Dу). Проведем секущую ММ₁ и обозначим угол наклона секущей к оси Ох через j: tgj=Dy/Dx

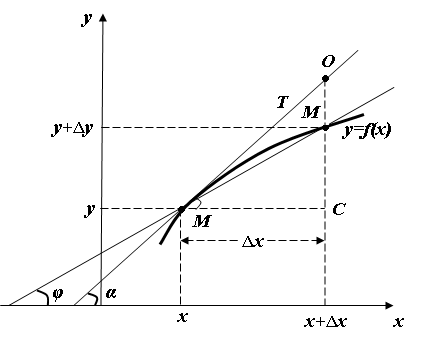
Рис 1. Геометрический смысл производной и дифференциала функции.

Пусть Dх®0, тогда точка М₁ будет стремиться к точке М, величина угла j будет изменяться. При приближении ММ₁ к касательной МТ, угол j приближается к углу a, следовательно, tga равен угловому коэффициенту касательной:

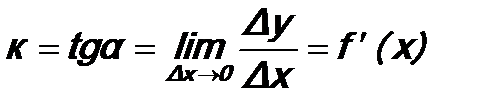
Таким образом, геометрический смысл производной заключается в том, что она есть угловой коэффициент касательной к графику функции в этой точке.