ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Пусть дана функция n-переменных:
Z = f (x, y, …, t)
В этом случае вводится понятие частной производной: 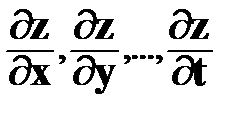
Частной производной функции Z=f (x, y) по аргументу х называется предел отношения приращения функции, когда изменяется х, к приращению аргумента  х, когда приращение аргумента стремится к нулю (
х, когда приращение аргумента стремится к нулю (  х → 0)
х → 0)
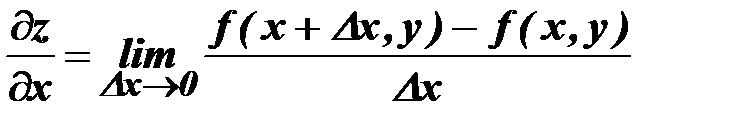
Соответственно частная производная по y обозначается 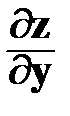 .
.
Если частную производную от функции Z = f(x, y) по х умножить на ее дифференциал dx, то получим частный дифференциал по аргументу х:
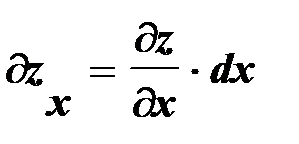
Частный дифференциал по у будет равен: 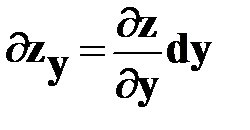
Сумма частных дифференциалов определяет полный дифференциал функции 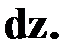
Полный дифференциал для функции двух переменных Z = f(x, y) равен:
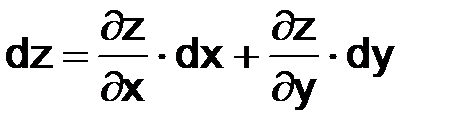
10. ПРИМЕНЕНИЕ ПОНЯТИЯ ДИФФЕРЕНЦИАЛА ФУНКЦИИ В ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЯХ
При достаточно малых |Dx| выполняется условие: Dy » dy.
Учитывая, что Dy = f(x0+Dx)-f(x0),
dy =f¢(x0)Dx, получаем
f(x0+Dx)-f(x0) » f¢(x0)Dx, откуда
f(x0+Dx) » f(x0)+f¢(x0) Dx (*)
Например: Вычислить приближённо 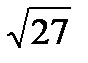 .
.
Решение: 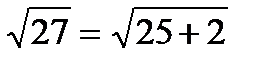 , тогда x0 =25, Dx=2. Применяя формулу (*), получаем:
, тогда x0 =25, Dx=2. Применяя формулу (*), получаем: 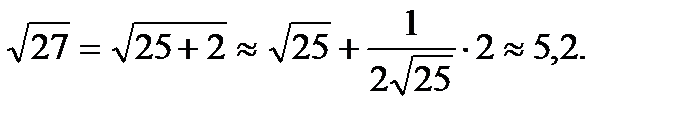
Дата добавления: 2016-06-05; просмотров: 4269;











