Эталоны решения типовых задач
Задача 1(а). Найти производную функции: 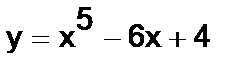 .
.
Решение: Для решения задачи необходимо применить правило дифференцирования алгебраической суммы: 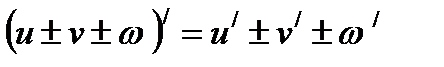 и формулу производной степенной функции:
и формулу производной степенной функции: 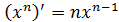 . Тогда получим:
. Тогда получим: 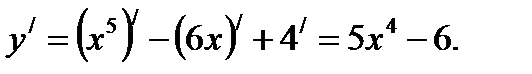
Ответ: 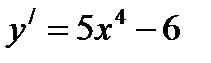
Задача 1(б). Найти производную функции: 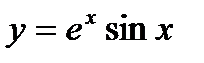
Решение: Применяя правило дифференцирования произведения функций 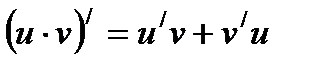 , находим
, находим
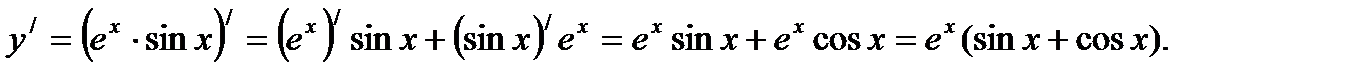
Ответ: 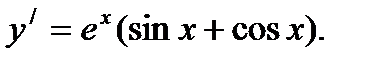
Задача 1(в) .Найти производную функции: 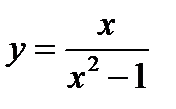 ; x2-1≠0.
; x2-1≠0.
Решение:Применяя правило дифференцирования частного функций: 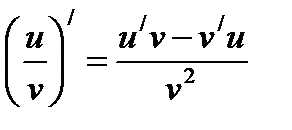 ; v≠0
; v≠0
находим: 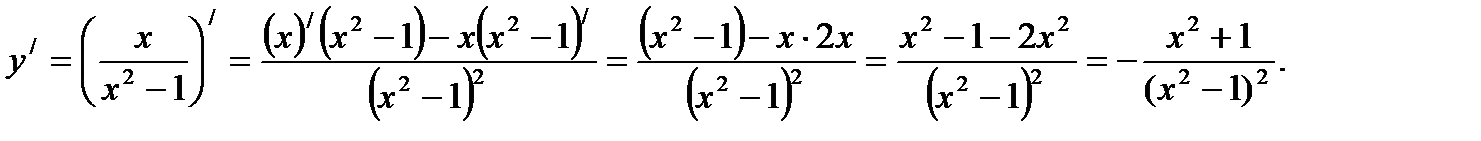
Ответ: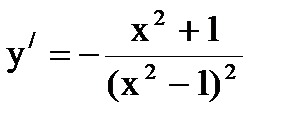
Задача 2(а). Найти производную функции: 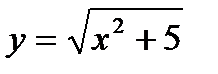 .
.
Решение: Данная функция может быть представлена в виде сложной степенной функции: 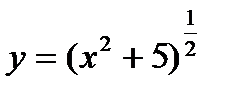 .
.
В соответствии с формулой производной сложной степенной функции: 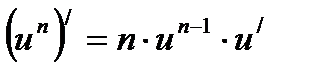 , имеем:
, имеем:
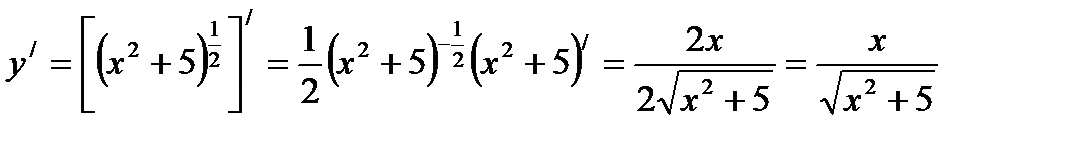 .
.
Ответ: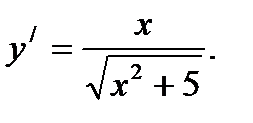
Задача 2(б). Найти производную функции: 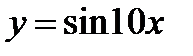
Решение: Применяем правило дифференцирования сложной функции: 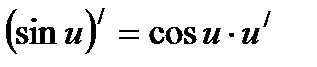 и имеем:
и имеем:
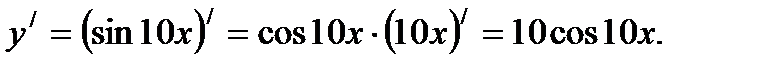
Ответ: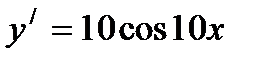
Задача 2(в). Найти производную функции: 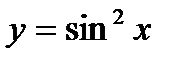 .
.
Решение: Данная функция является сложной и её производная определится следующим образом:
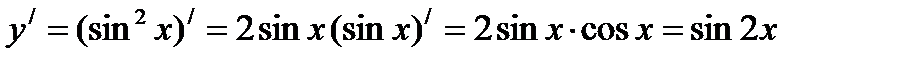 .
.
Ответ: 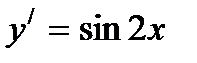 .
.
Задача 3(а). Найти производную второго порядка от функции: 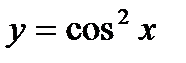 .
.
Решение: Находим первую производную: 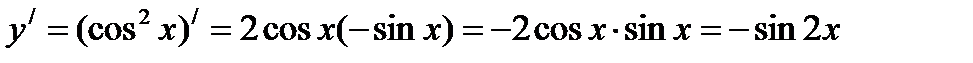 .
.
Зная, что производной второго порядка называется производная от производной первого порядка, получаем:
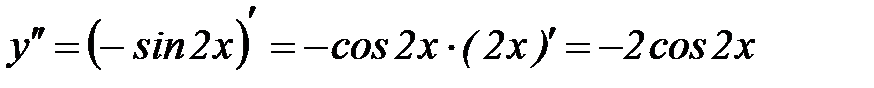
Ответ:- 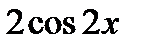
Задача 3(б). Точка движется по закону: x=t–sint. Определить мгновенные скорость и ускорение точки.
Решение: Мгновенная скорость точки характеризуется первой производной от смещения x по времени t: 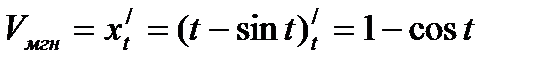 . Мгновенное ускорение точки характеризуется второй производной от смещения x по времени t или первой производной от скорости по времени:
. Мгновенное ускорение точки характеризуется второй производной от смещения x по времени t или первой производной от скорости по времени: 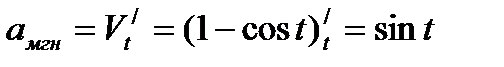 .
.
Ответ: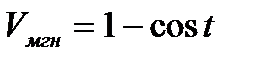 ;
;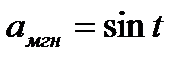 .
.
Задача 4. Определите зависимость градиента концентрации от координаты, если зависимость концентрации от координаты задана функцией: 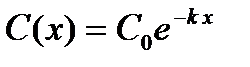 , где k - константа, а C0 есть концентрация вещества при x=0.
, где k - константа, а C0 есть концентрация вещества при x=0.
Решение: Величина градиента концентрации определяется выражением 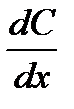 и характеризует быстроту изменения концентрации при изменении координаты. Пользуясь правилом дифференцирования сложной функции:
и характеризует быстроту изменения концентрации при изменении координаты. Пользуясь правилом дифференцирования сложной функции: 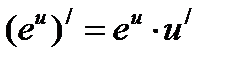 , в данном случае получим:
, в данном случае получим:
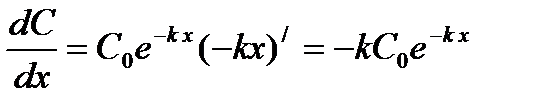 .
.
Ответ: величина зависимости градиента концентрации от координаты
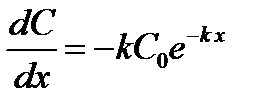 .
.
Задача 5. Найти дифференциал функции: 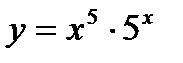 .
.
Решение: По определению 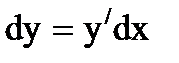 , т.е. чтобы найти дифференциал одной переменной, нужно найти производную
, т.е. чтобы найти дифференциал одной переменной, нужно найти производную 
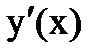 и умножить её на дифференциал аргумента dx. Искомый дифференциал будет:
и умножить её на дифференциал аргумента dx. Искомый дифференциал будет:
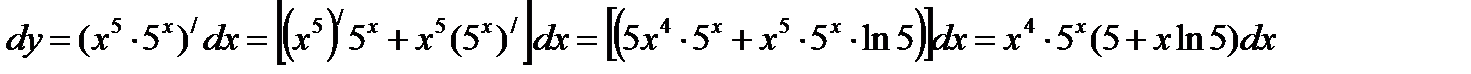
Ответ: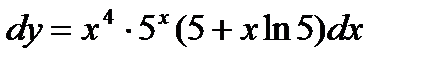 .
.
Задача 6.Найти полный дифференциал функции:
Z=3x2y3+8xy2-3y+ex.
Решение:
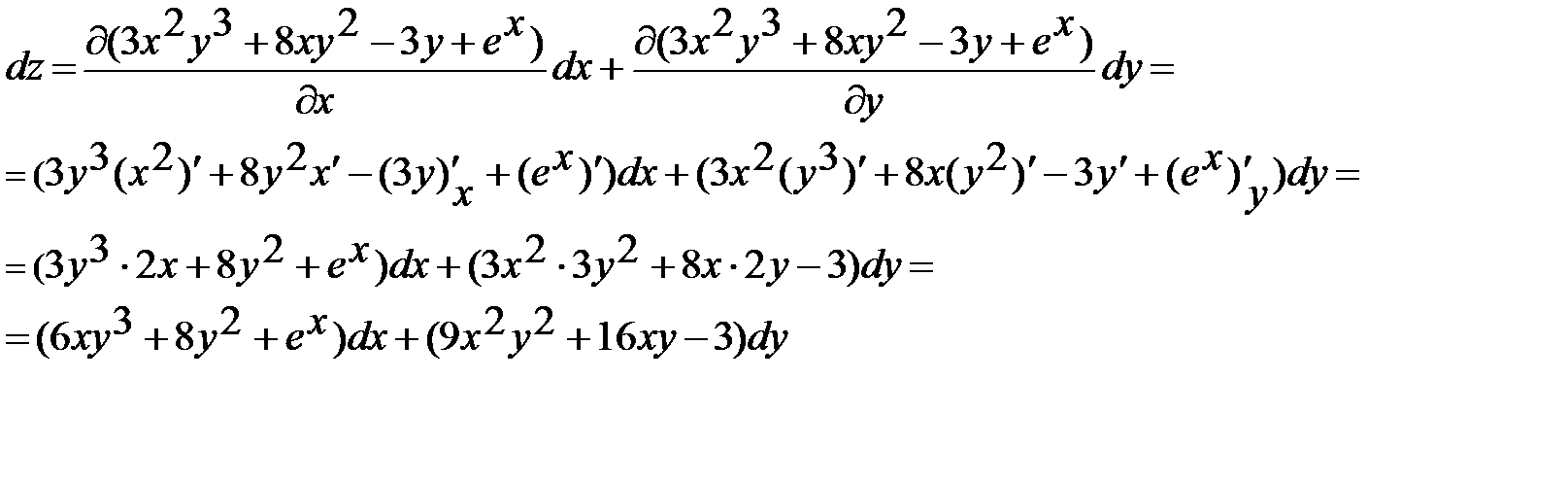
Дата добавления: 2016-06-05; просмотров: 3544;











