Сравнение эффективности способов восстановления непериодических сигналов
Для непериодических сигналов типа косинусоидального и экспоненциального импульсов (см. рис. 15.9) получены следующие соотношения (см. табл. 15.2).
А Б
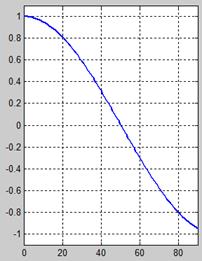
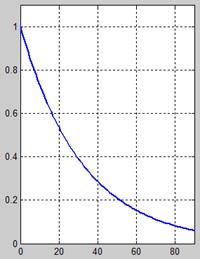
Рис. 15.8. Вид косинусоидального (А) и экспоненциального импульсов (Б)
Табл. 15.2. Необходимое количество отсчетов при различных способах восстановления
| Форма сигнала | Точность восстановления | Способ востановления | ||
| По Котельникову | Ступенчатая интерполяция | Линейная интерполяция | ||
| Косинусоидальный импульс | 0,1% | |||
| 1% | ||||
| Экспоненциальный импульс | 0,1% | |||
| 1% |
Видно, что для сигналов этого вида способ восстановления с помощью линейной интерполяции значительно более эффективен, чем способ восстановления «по Котельникову».
Примечание
Выбор необходимой частоты отсчётов сигнала зависит не только от вида сигнала, но и от решаемой средствами цифровой обработки задачи. Например, если решается задача определения разности фаз двух гармонических сигналов, то частота отсчётов может быть и меньше частоты Найквиста. Кроме того необходимо учитывать ограничения допустимой сложности алгоритма при аппаратной реализации системы ЦОС на основе цифрового сигнального процессора или ПЛИС.
ЛИТЕРАТУРА
1. Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., "Вильямс", 2004, 992 с.
2. Сергиенко А.Б. Цифровая обработка сигналов. Учебник для вузов. 2-е изд.-СПб.: Питер, 2006.-751с.
3. Юкио Сато Без паники! Цифровая обработка сигналов: Пер. с яп.. – М.: Изд. дом Додэка – XXI, 2010 - 176с.
4. Солонина А.И., Арбузов С.М.. Цифровая обработка сигналов. Моделирование в MATLAB: Учебное пособие. – СПб.: БХВ-Петербург, 2008 – 816с.
5. Тутыгин В.С. Цифровая обработка сигналов: лаб. практикум/ - СПб.: Изд-во Политехн. ун-та, 2015. – 116с.
6. Анищенко .В. Действующий макет средства радиотехнического контроля параметров РЛС с синтезированной апертурой антенны./Анищенко А.В., Катков Б.Г., Купряшкин И.Ф.,Попов В.Г., Рогов С.А., Тутыгин В.С., Яковлев Ю.В.// Вестник ВАИУ-2010 №4(11)-С.116-121.
7. А.В. Анищенко Акустооптоэлектронный приемник – анализатор спектра для измерения параметров радиосигналов в реальном масштабе времени / С.А. Рогов, М.Г. Высоцкий, Б.Г. Катков, В.А. Парфенов, С.В. Розов, В.В. Скороход, В.С. Тутыгин, А.В. Южаков // Радиотехника , №5, 2012 г.
8. Романюк Ю.А. Конспект лекций по цифровой обработке сигналов. /М.:МФТИ. 2016. https://mipt.ru/drec/forstudents/study/studyMaterials/5kurs.1/sign/f_28c5tb/
9. Тихонов А.Н.,Самарский А.А. Уравнения математической физики. Изд. 7, М.;МГУ, 2004.
10. Канатников А.Н., Крищенко А.П. Линейная алгебра. М.:Изд-во МГТУ им. Н.Э. Баумана, 2002 – 336с.
11. Макс. Ж. Методы и техника обработки сигналов при физических измерениях. В 2-х томах. М.: Мир, 1983,- 567с.
12. Марпл-мл.С.М. Цифровой спектральный анализ и его приложения: Пер. с англ. – М.:Мир, 1990 – 584с.
13. Тарханов В.И., Тутыгин В.С. Приборный комплекс для поиска и исследования сигналов ЯМР в магнитоупорядоченных веществах. // «Научное приборостроение», 2003, том 13, №1, с.58-63.
14. Тутыгин В.С.. Способ измерения частоты сигнала. Патент РФ на изобретение №2478213.
15. Тутыгин В.С.,Дебелова А.В. Новый метод частотного анализа. // Вестник СПбГУ, Серия 10 «Прикладная математика, информатика и процессы управления», №1, 2009.
16. Тутыгин В.С. Цифровая обработка коротких сигналов./В.С.Тутыгин - СПб.: Изд-во Политехн. ун-та, 2012. – 164с. ISBN 978-5-7422-3723-5.
17. Тутыгин В.С. Способ измерения временных интервалов между радиоимпульсами. Патент РФ на изобретение №2456632.
18. Тутыгин В.С. Способ повышения точности определения времени задержки зашумленных радиолокационных эхо-сигналов. // Научно-технические ведомости СПбГПУ. Серия Информатика. Телекоммуникации. Управление. 2011, №6.1(138)/2011,С. 220-225.
19. Тутыгин В.С., И. А. Пелконен И.А., Кириленко К.С. Способ и программная реализация прецизионного измерения времени задержки радиоимпульса. // Научно-технические ведомости СПбГПУ. Серия Информатика. Телекоммуникации. Управление. 2013, № 3(174).2013, С.123-128.
20. Huang, N. E., Z. Shen, S. R. Long, M. C. Wu, H. H. Shih, Q. Zheng, N.-C. Yen, С. C. Tung, and H. H. Liu, 1998: The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London, Ser. A, 454, 903-995.
21. Давыдов А.В. Теория сигналов и систем. http://prodav.narod.ru/signals/index.html
22. Давыдов А.В. Цифровая обработка сигналов. Конспект лекций. http://prodav.narod.ru/textbook/index.html
23. Басаргин И.В.,Мишин Г.И.,Федотов А.А. Автоматизированная установка для исследования динамических свойств ударных волн в газоразрядной плазме. Препринт 1642 ФТИ им. А.Ф.Иоффе РАН.
24. Давыдов В.А., Давыдов А.В. Очистка сигналов от шумов методом эмпирической модовой декомпозиции в диалоговом режиме. www.geoin.org/hht/app/hht6.doc
25. Тутыгин В.С.. Способ очистки сигналов от шумов с использованием неполной декомпозиции Хуанга //”Наука. Технологии. Производство”/ VI(10)/2015, стр 26-30, ISSN 2340-3499.
26. Мохаммед.Д., В.С. Тутыгин "Новый способ очистки сигналов от шумов на основе декомпозиции Хуанга"./Неделя науки СПБПУ: материалы научного форума с международным участием. Институт международных образовательных программ. –СПБ. Изд-во Политехн. ун-та,2015.-с.95-97.
27. Norden E/ Huang etc. On Instanteneous Frequency. Advances in Adaptive Data Analysis/ Vol. 1, No. 2 (2009) 177–229 World Scientific Publishing Company http://seichecostero.weebly.com/uploads/1/1/9/5/11950137/s1793536909000096.pdf
28. Сафиуллин Н.Т., Поршнев С.В. Сравнительный анализ расчета мгновенной частоты через преобразование Гильберта и прямую квадратуру. Научно-технические ведомости СПбГПУ » НТВ СПбГПУ. Информатика. Телекоммуникации. Управление » 2011 »Выпуск 5(133)/2011
29. Сафиуллин Н.Т. Разработка методики анализа временных рядов с помощью преобразования Хуанга-Гильберта. /Канд.дисс. Новосибирск, 2015.
30. Котельников В.А. О пропускной способности «эфира» и проволоки в электросвязи./ Материалы к I Всесоюзному съезду по вопросам технической реконструкции дела связи и развития слаботочной промышленности. 1933 г.
31. Paolo Prandoni, Martin Vetterli Digital Signal Processing// École Polytechnique Fédérale de Lausanne, Suisse, 2016. https://ru.coursera.org/learn/dsp
32. Яневич Ю.М. Задачи приема сигналов и определения их параметров на фоне шумов. Конспект лекций. Физический ф-т СПбГУ., http://www.phys.spbu.ru/library/studentlectures/yanevich.html
[1] У таких сигналов спектральная функция (преобразование Фурье) 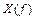 обращается в нуль вне некоторого конечного интервала частот, например,
обращается в нуль вне некоторого конечного интервала частот, например, 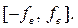
[2] Применяя метод ортогонализации Грама-Шмидта к системе линейно независимых функций мы получим систему других функций, в частности, применяя метод Грама-Шмидта к системе линейно независимых функций {1, t, t2, t3, …} мы приходим к системе полиномов Лежандра
[3] Монотонная функция – это функция, приращение которой не меняет знак, т.е. функция возрастающая или убывающая
[4] http://bourabai.kz/signals/ts0403.htm
[5] На интервале определения b(t) = 1-|t|/t, вне интервала b(t)=0.
[6] Если исходная функция h – линейная, К=2, если квадратичная - К=3.
[7] В зарубежных источниках данная теорема называется теоремой Найквиста (Nyquist theorem), теоремой Шеннона (Shannon theorem) или теоремой дискретизации (sampling theorem).
Дата добавления: 2017-01-16; просмотров: 2058;











