Применение разложения Хуанга для очистки нестационарного сигнала от шума.
Особенностью сигналов, получаемых при физических экспериментах, является то, что они, как правило, нестационарные и значительно зашумлены. Применение традиционных способов очистки сигналов от шумов с помощью частотных фильтров (сглаживающих, медианных, Баттерворта и др.) приводят к значительному искажению формы сигнала, что может приводить к ошибочной физической интерпретации изучаемого процесса.
Известен другой способ очистки сигналов от шумов, основанный на использовании эмпирической модовой декомпозиции Хуанга [22]. Способ заключается в разложении исходного сигнала на составляющие (моды), затем в исключении первых составляющих (от 1 до 3), которые обычно представляют собой шум, содержащийся в исходном сигнале.
На рис. 13.8 приведен пример зашумленного модельного сигнала, на рис. 13.9 - набор функций разложения и на рис. 13.10 - сигнал, очищенный от шума в результате вычитания первых трех функций разложения.
Основное достоинство данного способа очистки сигналов от шумов по сравнению с традиционными способами с использованием низкочастотных фильтров (сглаживающих, медианных, Баттерворта и др.) заключается в том, что фильтрация на основе эмпирической модовой декомпозиции значительно меньше искажает форму исходного сигнала.
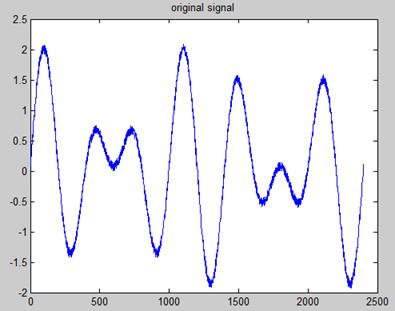
Рис. 13.8. Пример зашумленного модельного сигнала
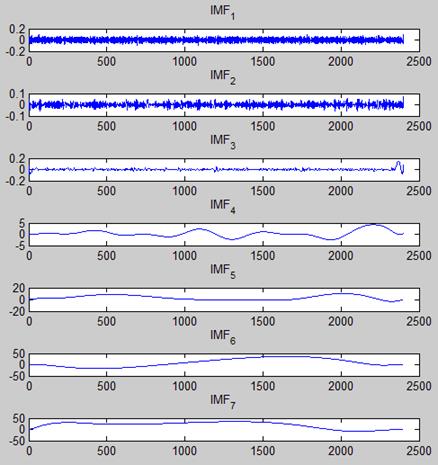
Рис. 13.10. Набор функций разложения зашумленного модельного сигнала
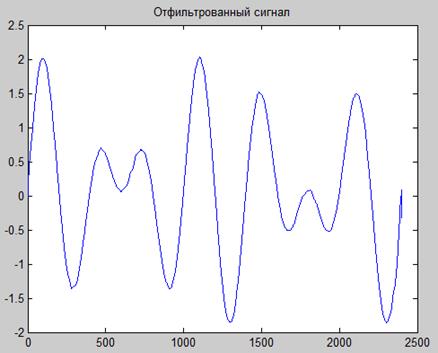
Рис. 13.10. Результат фильтрации, полученный вычитанием из исходного сигнала первых трех функций разложения
Опыт применения декомпозиции Хуанга для обработки значительно зашумленных сигналов, получаемых при физических экспериментах и приведенных в [23], показали, что:
· разложение Хуанга при различных реализациях шума становится неустойчивым, т.е. вид получаемых при разложении функций IMF существенно изменяется от опыта к опыту;
· количество функций IMF, представляющих собой шум, также изменяется от опыта к опыту: «шумовыми» могут быть как одна, так две, три и более функций. Между тем, коэффициент подавления шумов будет принимать приблизительно от 4 до 12, в зависимости от того, сколько «шумовых» IMF функций исключено. Это отмечается и в [22]. Естественно, желательно автоматически определять количество «шумовых» функций и исключать их все. Неправильное определение количества «шумовых» функций приводит или к недостаточной степени очистки сигнала от шума, или к значительным искажениям очищенного от шумов сигнала, поэтому исключать фиксированное количество функций IMF нельзя;
· в процессе декомпозиции происходит постепенное уменьшение количества экстремумов в функциях разложения и в связи с этим возникает проблема доопределения граничных значений функций IMF. Иначе это привело бы к значительным выбросам в области граничных значений, что, в свою очередь, привело бы к ошибочной физической интерпретации функций разложения и затруднило бы очистку сигнала от шумов. В [24] предлагается делать доопределение с помощью экстраполяции. В случае значительно зашумленного сигнала реализовать доопределение с помощью экстраполяции затруднительно.
Недостатки этого известного способа очистки сигналов от шумов на основе эмпирической модовой декомпозиции заключаются в сложности реализации доопределения граничных значений функций IMF и в отсутствии критерия для автоматического определения того, какие функции разложения могут рассматриваться как «шумовые».
Предлагаемый в [25] способ очистки сигналов от шумов включает чтение из файла исходного числового массива данных Y[j], j=1..N, N – количество точек дискретизации сигнала, определение локальных экстремумов Ymax[k] и Ymin[k] и номеров элементов jmax[k] и jmin[k] массива Y[j], соответствующих этим экстремумам, кубичную сплайн-интерполяцию массивов Ymax[jmax[k]] и Ymin[jmin[k]] и формирование массивов Ymax[j] и Ymin[j], j=1..N, вычисление функции средних значений M[j]= Ymax[j] -Ymin[j], j=1..N, вычисление первого приближения к первой функции моды H[j]=Y[j]-M[j], вычисление второго приближения к первой функции моды путем подстановки вместо Y[j] массива H[j] и повторения вычислений, вычисления третьего и последующих приближений к первой функции моды, при максимальном количестве приближений равном n, вычисление первого остатка R1[j] путем вычитания из исходного числового массива данных Y[j] n-го приближения к первой функции моды, вычисление второй и последующих функций моды Hs[j] и остатков Rs[j], s=1..n путем повторения вычислений путем подстановки вместо Y[j] массива Hs[j], s=1..n, доопределение граничных значений функций разложения по правилу Cs[1]=Cs[2], Cs[2]=1.1*Cs[3], Cs[3]=0.9*Cs[4], Cs[N]=Cs[N-1], Cs[N-2]=1.1*Cs[N-3], Cs[N-3]=0.9*Cs[N-4], чем обеспечивается формирование одного минимума и одного максимума в начале и в конце функции разложения, вычисление средних значений функций разложения Cssr, вычитание из исходного сигнала Y[j] тех функций разложения Cs, модуль среднего значения которых меньше порогового значения, определяемого как p*|C1sr|, p-множитель, пропорциональный уровню шума в обрабатываемом сигнале Y[j], j=1..N. Блок-схема алгоритма приведена на рис. 13.11.

Рис.13.11. Блок-схема алгоритма очистки сигнала от шумов на основе неполного разложения Хуанга
Отличительными признаками предлагаемого способа очистки сигнала от шума является то, что необходимое количество приближений к функции моды и необходимое количество функций разложения становится фиксированным и равным n, независимо от вида сигнала, причем значение n определяется степенью зашумленности сигнала, при малой зашумленности значение n может быть взято равным 4.
На рис. 13.12 приведены результаты очистки от шумов сигнала, отражающего изменение проводимости плазмы при воздействии на нее ударной волны, полученного при проведении плазмогазодинамического эксперимента в Физико-техническом институте РАН [23].
А Б

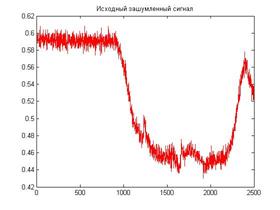
Рис. 13.12. Исходный зашумленный (А) и отфильтрованный сигнал (Б), полученные при проведении плазмогазодинамического эксперимента
Из рис. 13.12 видно, что в результате произведенной очистки тонкая структура исходного сигнала сохранена.
В [26] произведено сравнение эффективности фильтра, использующего разложения Хуанга, с частотными и усредняющими фильтрами. Результаты приведены в табл. 13.1 и на рис.13.13.
Табл13..1 Относительная погрешность сигнала на выходе фильтра от уровня шума на входе
| СКО шума на входе, % | |||||
| Вид фильтра | |||||
| Низкочастотный Фильтр | 0.335 | 0.43 | 0.59 | 0.55 | 0.74 |
| Фильтр скользящего среднего | 1.54 | 1.53 | 1.47 | 1.49 | 1.55 |
| Фильтр на основе EMD | 0.01 | 0.011 | 0.012 | 0.008 | 0.01 |
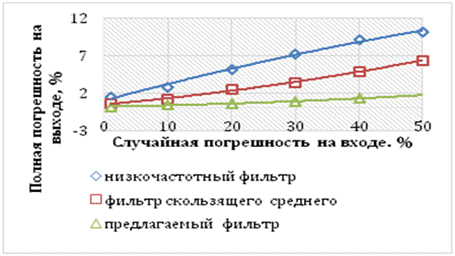
Рис.13.13 Результаты сравнения относительной погрешности сигнала на выходе фильтра от уровня шума на входе
Видно, что фильтр, основанный на EMD Хуанга, обеспечивает значительно большую степень подавления шумов, чем низкочастотный фильтр и фильтр скользящего среднего.
Дата добавления: 2017-01-16; просмотров: 2666;











