ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА
Сигналы, получаемые при проведении физических экспериментов, обычно являются нестационарными, значительно зашумлены и имеют сложную форму, что затрудняет физическую трактовку изучаемых процессов. Частотный анализ сигналов с помощью преобразования Фурье, представляющий сигнал в виде суммы гармонических составляющих, не улучшает возможность трактовки изучаемых процессов.
Эмпирическая модовая декомпозиция Хуанга позволяет представить сигнал в виде суммы (до 10) колебательных нестационарных составляющих, для частотного анализа каждого из которых может быть применено преобразование Гильберта.
Преобразование Гильберта позволяет представить каждую компоненту разложения Хуанга в частотно-временном пространстве. Каждому моменту времени будет соответствовать мгновенная частота сигнала.
Спектральный анализ Гильберта (HSA) применяется для описания нестационарных сигналов, т.е. сигналов с меняющейся во времени амплитудой и фазой. Для выделения амплитуды и фазы произвольный сигнал s(t) представляется как вещественная часть комплексного сигнала

Комплексный сигнал называют аналитическим сигналом.
Вещественная часть аналитического сигнала, естественно, должна совпадать с исходным сигналом s(t). Мнимую же часть Hs(t) называют сопряженным сигналом и вычисляют с помощью преобразования Гильберта
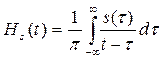
Это приводит к аналитическому сигналу z(t) = s(t)+j Hs(t) .
Отсюда может быть определена мгновенная амплитуда a(t) и мгновенная фаза 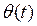 сигнала:
сигнала:

Мгновенная частота может быть вычислена по формуле
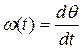
Дата добавления: 2017-01-16; просмотров: 2101;











