Выбор шага квантования по уровню DX
Выбор шага квантования по уровню DX производится из условия достижения необходимой точности восстановления значений непрерывного измеряемого сигнала в ЭВМ по дискретным отсчетам.
 |
Погрешность восстановления может быть оценена максимальной и среднеквадратической ошибкой
учитывая, что закон распределения ошибки квантования – равномерный.
 |
Исходя из уровня допустимой погрешности восстановления, условие выбора шага квантования по уровню можно записать в виде
 |
Условие оптимального выбора шага квантования, при котором и младший разряд АЦП несет полезную информацию,
Выбор шага квантования в диапазоне Xmin – Xmax определяет разрядность АЦП. Необходимое количество уровней квантования N АЦП в диапазоне изменения входного сигнала Xmin – Xmax равно
 |
а количество разрядов выходного кода
n=log2N
Расчёт интервала дискретности по времени
 |
Погрешность восстановления зависит от характера непрерывного сигнала X(t) и от используемого способа восстановления. Для восстановления используются интерполяционные и описана и фильтрационные способы. Наиболее часто используется восстановление по теореме Котельникова , ступенчатая, линейная интерполяция и кубичная сплайн-интерполяция.
а)восстановление по теореме Котельникова[7]
Возможность полной реконструкции непрерывного сигнала по дискретным отсчетам была доказана впервые и опубликована в [30] Котельниковым В.А. в его теореме: «Любую функцию {\displaystyle f(t)\;}f(t), состоящую из частот от 0 до {\displaystyle f_{c}\;}fc, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через {\displaystyle 1/(2f_{c})\;}1/(2 fc) секунд».
Другими словами непрерывный сигнал может быть восстановлен абсолютно точно по дискретным отсчетам, если:
· непрерывный сигнал имеет ограниченный частотный спектр;
· отсчеты взяты через равные интервалы времени;
·
 |
частота отсчетов превышает не менее, чем вдвое, максимальную частоту в спектре непрерывного сигнала
Эту частоту отсчетов, вдвое превышающую максимальную частоту в спектре непрерывного сигнала, называют частотой Найквиста. Восстановление значений непрерывного сигнала необходимо производить по формуле:
 |
 |
В результате каждому значению дискретизированного сигнала будет посталена в соответствие функция sinc (рис. 10.3) – кардинальный синус, называеваемая базисом Котельникова. (см. примеры на рис. 15.2 и 15.3).
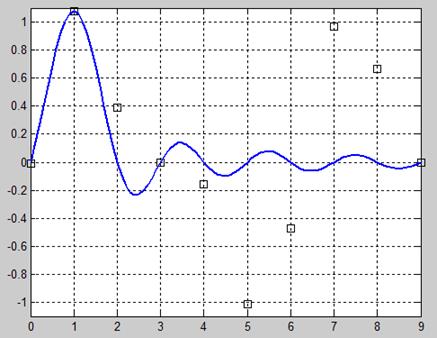
Рис. 15.2. Пример 1 замены одного дискретного значения сигнала функцией sinc
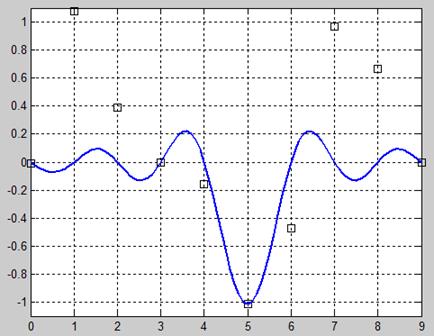
Рис. 15.3. Пример 2 замены одного дискретного значения сигнала функцией sinc
После суммирования таких функций получим точное восстановление исходного непрерывного сигнала по дискретным отсчетам (см. рис. 15.4 и 15.5).
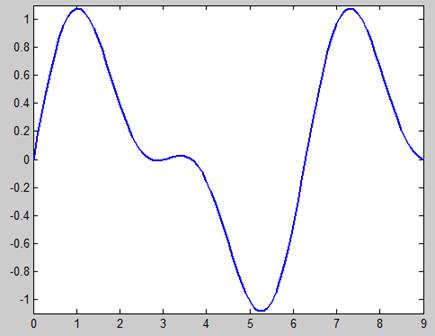
Рис. 15.4. Исходный сигнал X(t)
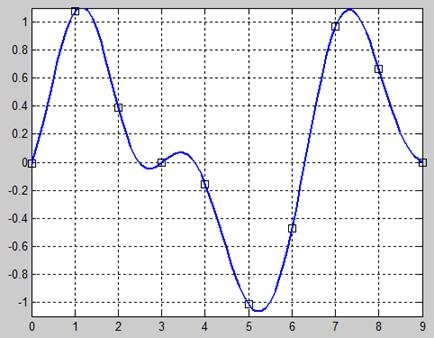
Рис. 15.5. Сигнал, восстановленный «по Котельникову»
Реализовать абсолютно точное восстановление непрерывного сигнала по дискретным отсчетам с использованием базиса Котельникова, однако, невозможно по следующим причинам:
· Сигналы могут иметь бесконечный частотный спектр;
· Значения X(lDt) известны с погрешностью.
Примечание
Частотный спектр сигнала вычисляется для всего сигнала, имеющего бесконечную длительность, составленного из фрагментов ограниченной длительности, аналогичных показанным на рис. 15.4. Спектры отдельных фрагментов могут содержать сколь угодно высокие частоты, а спектр всего сигнала при этом может иметь ограниченный частотный спектр [2].
Условием ограниченности частотного спектра всего сигнала является равенство начадьного и конечного значения фрагмента сигнала. Если это условие не выполнено, спектр всего сигнала будет иметь бесконечный частотный спектр и точное восстановление сигнала с помощью базиса Котельникова будет невозможно.
б) с помощью ступенчатой интерполяции
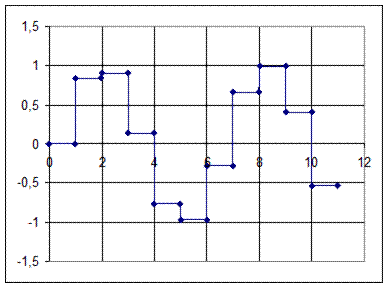
Рис. 15.6. Сигнал, восстановленный с помощью ступенчатой интерполяции
 |
При использовании ступенчатой интерполяции восстановление непрерывного сигнала по дискретным отсчетам производится по формуле:
Погрешность восстановления может быть оценена величиной
 |
 |
Отсюда
Для гармонического сигнала
 |
 |
имеем:
Отсюда
в) с помощью линейной интерполяции.
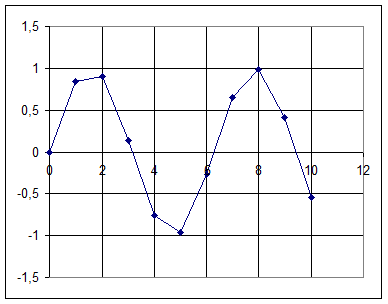
Рис. 15.7. Сигнал, восстановленный с помощью линейной интерполяции
При использовании линейной интерполяции восстановление
непрерывного сигнала по дискретным отсчетам производится по формуле:
 |
 |
Погрешность восстановления можно оценить величиной остаточного члена разложения в ряд Тейлора:
Отсюда
 |
 |
Для гармонического сигнала
 Отсюда
Отсюда
 |
г) с помощью кубичной сплайн-интерполяции
Сплайн-интерполяция используется для представления данных отрезками полиномов невысокой степени — чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Из этого вытекают следующие свойства кубической сплайн-интерполяции:
· график кусочно-полиномиальной аппроксимирующей функции проходит точно через узловые точки;
· в узловых точках нет разрывов и резких перегибов функции;
· благодаря низкой степени полиномов погрешность между узловыми точками обычно достаточно мала;
· связь между числом узловых точек и степенью полинома отсутствует;
· поскольку используется множество полиномов, появляется возможность аппроксимации функций с множеством пиков и впадин.
График интерполирующей функции при этом виде интерполяции можно уподобить кривой, по которой изгибается гибкая линейка, закрепленная в узловых точках.
Оценку погрешности при кубичной сплайн-интерполяции дает следующее выражение
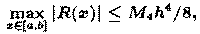
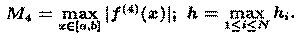
Отсюда получаем условие выбора шага дискретности по времени:
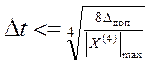
Дата добавления: 2017-01-16; просмотров: 2789;











