Выполнение преобразования Гильберта в MATLAB

Для выполнения преобразования Гильберта предусмотрена функция hilbert :

hx=hilbert(h),

где

h – массив входного (нестационарного сигнала s(i), i=1,..n;

hx – вычисленный массив сопряженного сиграла Hs(i).

Для вычисления мгновенной фазы сигнала предусмотрена функция angle:

phi=angle(hx)

Вычисление функции мгновенной частоты может производиться с путем численного дифференцирования функции фазы, например

f=diff(phi).

Однако это приводит к неправильным результатам (см. рис.14.1)

Рис. 14.1

Одна из причин плохих результатов заключается в том, что в точках разрывов функции фазы MATLAB считает производную отрицательной. Для устранения этой проблемы можно заменить отрицательные значения производной на предыдущие:

f=diff(phi);

for i=1:n-1

if (f(i)<0)

f(i)=f(i-1);

end

end

Однако и это не дает хорошего результата (см. рис.14.2).

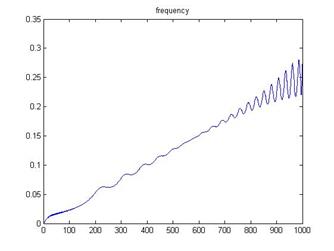
Рис. 14.2

Это связано с тем, что функция diff в MATLAB использует конечные разности для вычисления производных; она непригодна для работы с функциями, имеющими разрывы.

Для устранения разрывов функции в MATLAB предусмотрена функция unwrap. Она корректирует фазовые углы элементов одномерного массива при переходе через значения 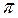, дополняя их значениями 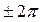. Строка программы:

phi2=unwrap(phi).

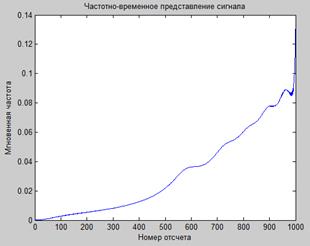
Рис. 14.3

Но и этого оказывается недостаточно. Перед вычислением производной функцию phi2, полученную в результате применения unwrap, необходимо аппроксимировать полиномом. В итоге программа вычисления функции мгновенной частоты на основе преобразования Гильберта будет иметь вид:

hx=hilbert(h);

phi=angle(hx);

phi2=unwrap(phi);

p=polyfit(0:n-1,phi2,K);% аппроксимация полиномом степени К[6]

dp=polyder(p);%вычисление производной

f=polyval(dp,0:n-1);вычисление функции мгновенной частоты

Ниже приведён пример программы, вычисляющей функцию мгновенной частоты для сигнала с квадратичным изменением частоты.

n=1000; % количество отсчетов

k=5 ; % количество периодов

h=zeros(1,n);

for i=1:n

% h(i)= sin(3*pi*k*i*i/n/n);%линейная частотная модуляция (ЛЧМ)

h(i)=sin(2*pi*k*i*i*i/n/n/n); %квадратичная частотная модуляция

end

figure

plot(h)

title('Исходный сигнал')

xlabel('Номер отсчета');

hx=hilbert(h); %преобразование Гильберта

phi = angle(hx); %фаза

phi2 = unwrap(phi);

p = polyfit(0:n-1,phi2,3); %аппроксимация полиномом третьей степени

dp = polyder(p); %производная полинома

f = polyval(dp, 0:n-1); %Вычисление значений полинома

figure

plot(f)

title('Частотно-временное представление сигнала')

xlabel('Номер отсчета');

ylabel('Мгновенная частота');

pause

close all;

clear;

Результат работы программы представлен на рис.14.4.

А Б

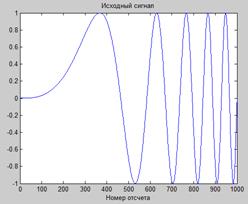
В Г

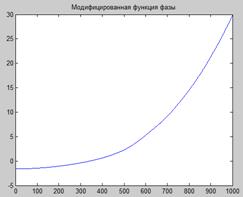
Рис. 14.4. Исходный сигнал (А), функция фазы, вычисленная с помощью преобразования Гильберта (Б, В), и функция мгновенной частоты.

Примечание

Для получения правильного результата (квадратичной зависимости частоты от времени в исходном сигнале соответствует вычисленная с помощью преобразования Гильберта квадратичная функция мгновенной частоты) необходимо, чтобы исходный сигнал содержал не менее одного периода и количество отсчётов за период было не менее 10.

Поэтому достоверность полученной зависимости при анализе сложного нестационарного сигнала может быть обеспечена только при разбиении сигнала на фрагменты, в каждом из которых сигнал аппроксимируется полиномом не выше 3-го порядка, и изложенное выше условие выполнено.

В [27] описан, а в [28-29] исследован альтернативный преобразованию Гильберта предложенный Хуангом метод прямой квадратуры, позволяющий производить вычисление функции мгновенной частоты сигнала.