ОПТИМАЛЬНАЯ И СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ

Оптимальная фильтрация

Оптимальное выделение сигнала из шума можно проводить различными методами, в зависимости от того, какая задача ставится: обнаружение сигнала, сохранение формы сигнала и т.д. В каждом методе оптимальной фильтрации вводится понятие критерия оптимальности, согласно которому строится оптимальный алгоритм обработки сигнала.

Передаточная функция оптимального фильтра, предназначенного для обнаружения прямоугольного импульса длительностью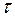

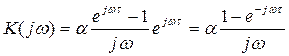
Блок-схема устройства

Рис.9.1. Блок-схема оптимального фильтра, предназначенного для обнаружения прямоугольного импульса длительностью 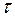. 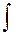- интегратор, 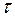- элемент временной задержки.

А Б

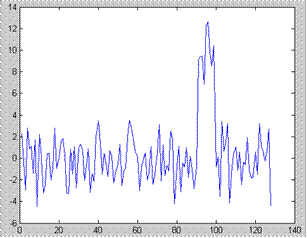
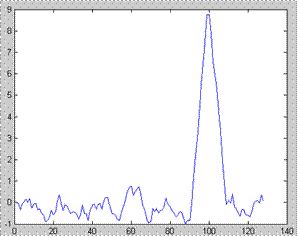
Рис. 9.2. Входной зашумленный прямоугольный импульсный сигнал (А) и выходной сигнал оптимального фильтра (Б).

Оптимальный фильтр в данном случае решает задачу обнаружения одиночного импульса конечной длительности. Форма и амплитуда импульса после фильтра будут искажены.

Оптимальный фильтр Колмогорова-Винера

Фильтры низкой частоты, высокой частоты и полосовые фильтры эффективны в том случае, когда частотные спектры сигнала и шума не перекрываются.

Наилучшее разделение сигнала и шума цифровыми методами обеспечивает оптимальный фильтр Колмогорова-Винера.

Частотная характеристика фильтра Колмогорова-Винера:

H(w) = Ws(w) / [Ws(w)+Wq(w)]

где Ws(w) и Wq(w) - энергетические спектры (плотности мощности) сигнала и помех.

На рис. 9.3 и 9.4 приведены примеры фильтрации сигналов вида одиночного импульса и синусоидального сигнала ограниченной длительности.

А Б

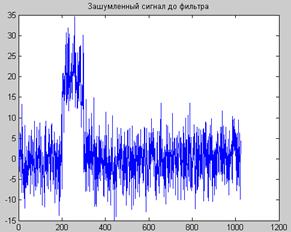
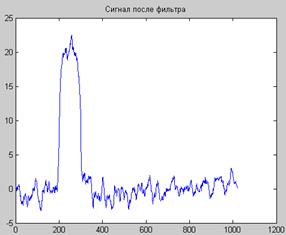
Рис. 9.3. Исходный сигнал с шумом (А) и после фильтра (Б).

А Б

Рис. 9.4. Частотная характеристика оптимального фильтра (А) и сигнал после фильтрации гармонического сигнала (Б).

Программа оптимального фильтра Колмогорова - Винера

Y=fft(s1,N)/N; %БПФ сигнала без шума

SS1=Y.*conj(Y)/N; %спектр мощности сигнала без шума

Y1=fft(q,N)/L; %БПФ шума

SS2=Y1.*conj(Y1)/N; %спектр мощности шума

for i=1:N

H(i)=SS1(i)/(SS1(i)+SS2(i)); %передаточная функция оптимального %фильтра в частотной области

end

i=1:N

XX1=fft(x1,N); %частотный спектр сигнала с шумом

Z=ifft(XX1.*H); %свертка зашумленного сигнала с частотной характеристикой фильтра

Согласованная фильтрация

Цифровая обработка сигналов решает две основные задачи: обнаружение и определение параметров зашумленного сигнала. Задача может состоять и только в обнаружении сигнала, вид которого известен. В этом случае может быть использована согласованная фильтрация, т.е. применен фильтр, «настроенный» точно под ожидаемый вид сигнала.

Для того, чтобы вычислить выходной сигнал фильтра, нужно выполнить операцию свертки массива частотного спектра F входного сигнала с частотной характеристикой фильтра H с помощью функции обратного преобразования Фурье, например, Z=ifft(F.*H), или операции свертки массива входного сигнала x с импульсным откликом фильтра h, например: Z = conv(x,h).

Частотная характеристика согласованного фильтра вычисляется "по частотному спектру сигнала" как комплексно сопряженный массив с помощью функции conj, например: Kf=conj(F). Здесь F- частотный спектр сигнала, Kf-частотная характеристика фильтра, согласованного с этим сигналом.

Ниже на рис. 9.5 приведен пример использования согласованного фильтра для определения временного интервала между радиоимпульсами.

А Б

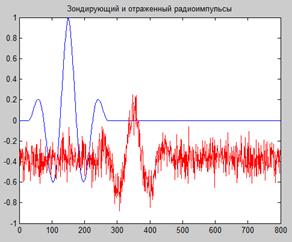
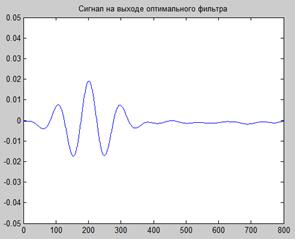
Рис.9.5. Зондирующий и отраженный сигналы (А) и сигнал на выходе согласованного фильтра.

Положение максимума выходного сигнала согласованного фильтра показывает величину временной задержки между зондирующим и отраженным импульсами.

Фрагмент программы согласованного фильтра для определения временной задержки между импульсами можеи иметь вид:

F1=fft(x,kt); % БПФ зондирующего радиоимпульса

Kf=conj(F1); % частотная характеристика согласованного фильтра

F2=fft(y,kt); % БПФ отраженного радиоимпульса

Fv=F2.*Kf; % свертка спектра отраженного радиоимпульса с частотной характеристикой согласованного фильтра.

Sv=real(ifft(Fv)); % вычисление сигнала после фильтра

Ниже приведен еще один пример использования согласованного фильтра для обнаружения линейно-частотно-модулированного сигнала (ЛЧМ-сигнала). Здесь цифровая обработка применяется не к самому ЛЧМ-сигналу (рис.9.6А), а к его частотному спектру, который представляет собой широкополосный сигнал в частотной области ( рис. 9.6Б).

А Б

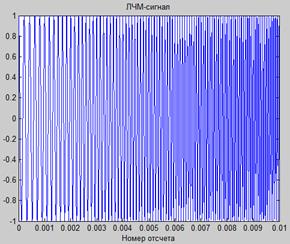
Рис. 9.6. Вид ЛЧМ-сигнала (А) и его частотного спектра (Б)

На рис. 9.7А приведен вид сигнала на выходе согласованного фильтра для случая, когда ЛЧМ-сигнал точно соответствует по форме тому, на который настроен фильтр. При зашумлении ЛЧМ-сигнала или его спектра форма отклика на выходе согласованного фильтра сохранится (см. рис. 9.7Б), что и дает возможность обнаруживать ЛЧМ-сигнал на фоне шумов .

Обратите внимание, что форма сигнала, полученного с выхода согласованного фильтра, не имеет ничего общего с формой ЛЧМ-сигнала (и определить параметры ЛЧМ-сигнала по нему невозможно). Кроме того, если

Рис. 9.7. Пример выходного сигнала согласованного фильтра при незашумленном (А) и зашумленном (Б) сигнале на входе

ЛЧМ-сигнал будет отличаться по ширине полосы или по центральной частоте от того, на который "настроен" согласованный фильтр, то определить параметры ЛЧМ-сигнала по выходному сигналу согласованного фильтра будет еще более сложно (см. рис. 9.6). На рис. 9.8А приведен вид выходного сигнала согласованного фильтра для случая, когда ЛЧМ-сигнал отличается по ширине полосы, на рис. 9.8Б - по ширине полосы и по центральной частоте.

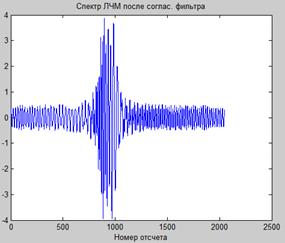
Рис. 9.8. Вид выходного сигнала согласованного фильтра для случаев, когда ЛЧМ-сигнал отличается по ширине полосы (А) и по ширине полосы и по центральной частоте (Б).