Квазиоптимальная фильтрация
Реализовать оптимальный согласованный фильтр вида (5.31) или для спектра (5.32) практически сложно, поэтому применяют метод квазиоптимальной фильтрации.
Впервые этот метод предложил Сифоров В.И. Метод квазиоптимальной фильтрации основан на введении понятия эффективной полосы сигнала.
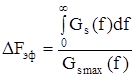 . (5.33)
. (5.33)
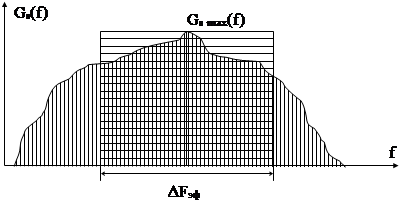 |
Рис. 5.12
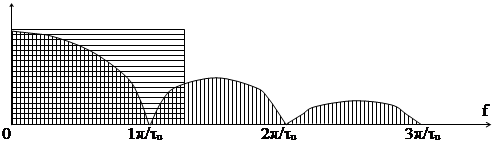 |
Рис. 5.13
В.И.Сифоров рассмотрел квазиоптимальное согласование прямоугольного видеоимпульса с идеализированным фильтром с прямой частотной характеристикой и определил эффективную полосу:
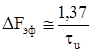 . (5.36)
. (5.36)
При этом отношение сигнал/шум мощности:
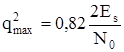 , (5.36)
, (5.36)
т.е. снижение отношения сигнал/шум на 0,18 по сравнению с (5.29). Для выравнивания отношения необходимо увеличить энергию сигнала в 1,22 раза (меньше 1 дБ). При этом полоса прямоугольного фильтра некритична – при изменении ее в 1,5 раза проигрыш увеличивается до 1,25 раза (т.е. в пределах 1 дБ). Применение квазиоптимальной фильтрации при незначительном проигрыше дало возможность достаточно просто реализовать согласованную фильтрацию.
Еще проще оказать реализовать квазиоптимальную фильтрацию для прямоугольного импульса другим фильтром – фильтром низких частот.
Частотную характеристику фильтра низких частот, показанного на рис. 5.14, имеет простейшая RC-цепь.
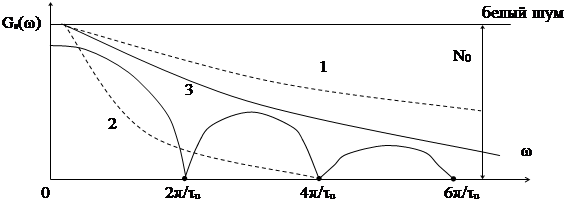 |
Рис. 5.14
 |
Рис. 5.15
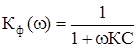 .
.
Т = RC – постоянная времени фильтра, от ее величины зависит скорость убывания частотной характеристики (1, 2, 3). Понятно, что частные характеристики 1 и 3 не оптимальны, в первом случае через фильтр проходит много шума, во втором – на выход фильтра поступает мало энергии сигнала.
Максимальным значение сигнала на выходе цепи RC для прямоугольного импульса Uвых(t) будет в момент времени t = τu, т.е.
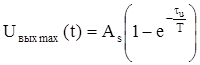 ,
,
где As – амплитуда.
Средняя плотность мощности белого шума на выходе RC цепи равна:
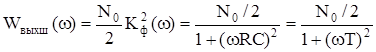 ,
,
где 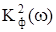 - квадрат модуля коэффициента передачи интегрирующей RC цепи по напряжению.
- квадрат модуля коэффициента передачи интегрирующей RC цепи по напряжению.
Спектральная плотность "белого" шума обозначается как N0 при оценке шума в полосе частот от 0 до ∞ и равна N0/2 при оценке шума в полосе от -∞ до +∞. Сейчас шум будем рассматривать в полосе от -∞
до +∞, т.е. через выражение N0/2.
На выходе цепи дисперсия шума будет:
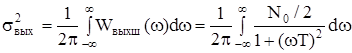 .
.
Решение интеграла 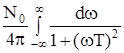 находится из известной формулы:
находится из известной формулы:
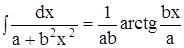 .
.
Применительно к нашему случаю будет:
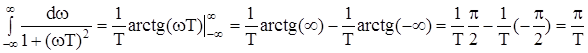 .
.
и окончательно:
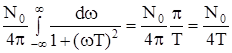 ,
,
отсюда
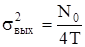 .
.
Отношение сигнал/шум на выходе цепи по мощности:
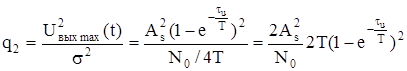
домножим на 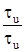
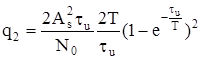
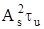 - представляет энергию сигнала Es.
- представляет энергию сигнала Es.
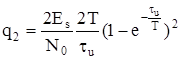 .
.
Выражение (5.28) 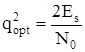 соответствует максимальному отношению сигнал/шум оптимального фильтра. Оценим изменение этого отношения для анализируемого квазиоптимального фильтра пронормировав его по
соответствует максимальному отношению сигнал/шум оптимального фильтра. Оценим изменение этого отношения для анализируемого квазиоптимального фильтра пронормировав его по 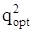 (разделив q2 на
(разделив q2 на 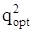 ):
):
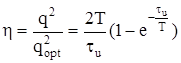 . (5.38)
. (5.38)
Исследуя на экстремум (максимум) выражение (5.38) в зависимости от отношения Т/τu, можно легко установить, что максимальное значение η будет при Т/τu = 1, т.е. при Т = τu и оно будет равно:
η = 2(1-е-1) = 0,798 ≈ 0,8.
Это говорит о том, что отношение сигнал/шум квазиоптимального RC фильтра немного хуже, чем оптимального (~0,8), однако его реализация крайне проста.
Исследуя влияние отношения T/τu на отношение сигнал/шум, нетрудно вычислить график этой зависимости (изменение постоянной времени T = RC отражены на рис. 5.14, кривые 1 и 2).
Рассчитанный по формуле (5.38) график зависимости отношения сигнал/шум от отношения T/τu приведен на рис. 5.15.

Рис. 5.15
* Интеграл Гаусса 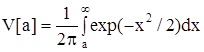
Дата добавления: 2016-06-18; просмотров: 4586;











