ЦИФРОВАЯ ОБРАБОТКА КОРОТКИХ СИГНАЛОВ. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ СИГНАЛА.

Одной из важнейших задач цифровой обработки зашумленных сигналов является обнаружение информативного сигнала в потоке данных, искаженных шумами и помехами, и определение его параметров. Для этого применяются различные методы, такие как временная фильтрация (накопление), оптимальная частотная фильтрация, прямое и обратное преобразование Фурье, корреляционная обработка. Каждая из этих операций позволяет выполнять преобразования исходного сигнала, например, переход сигнала из временной области в частотную или наоборот, причём при этом производится уменьшение уровня шумов в обработанном сигнале. В задачах обнаружения и определения параметров зашумлённых сигналов усиление эффекта подавления шумов и увеличения точности определения параметров сигнала можно достичь, используя несколько методов цифровой обработки в комплексе. Примером может быть задача обработки эхо-сигнала спектрометра ЯМР.

Результатом БПФ дискретизированного эхо-сигнала спектрометра ЯМР определенной частоты является количество пери­одов сигнала во временном окне. Если частота отсчетов или интервал дискретности по времени при измерении сигнала известен, то по количеству периодов во временном окне можно установить и частоту измеряемого сигнала. Точность определения частоты в спектре входного сигнала вполне определенна и зависит от количества периодов p сигнала. Если количество периодов целое, то частота с помощью БПФ находится точно (даже при наличии значительной зашумленности сигнала). Если же ко­личество периодов p не является целым, то появляется погрешность определения частоты. Максимальное значение погрешности равняется 1/2p [12]. В некоторых, практически важных случаях, например, при обработке эхо-сигналов (рис. 11.1) импульсных спектрометров ЯМР, количество периодов анализируемого сигнала во временном окне принципиально ограничено величиной около 10 [13]. В этом случае погрешность определения частоты с помощью БПФ достигает 1/10, т. е. 10%.

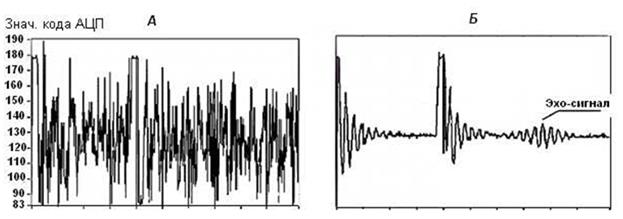
Рис. 11.1. Исходный (А) и накопленный (Б) эхо-сигнал в борате железа FeBO₃ .

Непосредственное использование БПФ не позволяет получить точное значение количества периодов во временном окне и частоты измеряемого сигнала в том случае, когда количество периодов не является целым, когда анализируемый сигнал занимает только часть временной области, модулирован по амплитуде и зашумлен. В практически важных случаях частотного анализа сигналов спектрометров ЯМР форма и начальная фаза эхо-сигналов известны, неизвестна и требует определения лишь частота. Это дает возможность создать эталонные сигналы, соответствующие ожидаемому эхо-сигналу по форме и начальной фазе, и произвести их корреляционное сравнение. Коэффициент корреляции эхо-сигнала с эталонным сигналом будет равен единице, если частоты эхо-сигнала и эталонного сигнала равны и эхо-сигнал не зашумлен. Поэтому при отсутствии шумов найти частоту эхо-сигнала можно производя корреляционное сравнение с эталонными сигналами, частоту эталонных сигналов подбирать до выполнения условия, когда коэффициент корреляции будет равен единице. Однако коэффициент корреляции уменьшается как при разнице частот эхо и эталонного сигналов, так и при совпадении частот, но из-за наличия шума. Поэтому таким способом определить частоту зашумленного сигнала невозможно.

Повышение точности определения частоты сигнала может быть достигнуто за счет сочетания положительных качеств корреляционного подхода и БПФ.

Идея способа, описанного в [14 - 16], заключается в том, что вычисляются коэффициенты корреляции исходного сигнала с несколькими эталонными, отличающимися по частоте в некоторой окрестности от приближенного значения частоты, затем с помощью сплайн-аппроксимации строится функция, выражающая зависимость коэффициентов корреляции исходного сигнала с эталонными от частоты эталонов, и находится положение максимума этой функции, которое определяет уточненное значение частоты исходного сигнала. Функция, построенная таким образом, имеет вид параболы с явно выраженным максимумом (см. рис. 11.2) как в случае незашумленного так и зашумленного сигнала, что и позволяет определить частоту эхо-сигнала более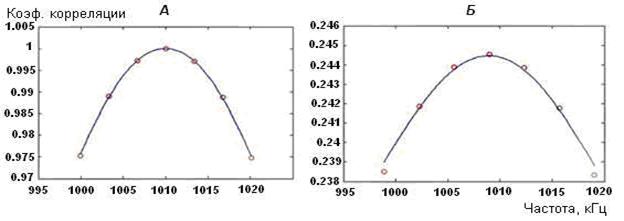

Рис. 11.2. Зависимость коэффициента корреляции от частоты при отсутствии шума (А) и при отношении сигнал/шум 1/3 (Б). Точное значение частоты равно 1010. Аппрок­симирующие кривые построены с помощью функции сплайн-аппроксимации spaps в MATLAB.

точно, чем это позволяет сделать БПФ. При наличии шума форма функции сохраняется, уменьшается лишь абсолютное значение максимума. Более точное определение положения максимума, т.е. частоты сигнала может быть найдено благодаря передискретизации. В результате сплайн-аппроксимации мы получаем функциональную зависимость. Это дает возможность создать числовой массив на анализируемом участке частотного спектра с шагом меньшим единицы, например, с шагом 0.1, т.е. произвести передискретизацию. В этом числовом массиве можно найти положение максимума функции, полученной с помощью сплайн-аппроксимации в К раз более точно, если шаг дискретизации был уменьшен в К раз.

Допустим, в исходном массиве положение максимума было на частоте 1010, а после сплайн-аппроксимации функции кросскорреляции и передискретизации положение максимума стало 1010.3.

Размер окрестности вблизи приближенного значения частоты, найденного, например, с помощью БПФ, должен быть выбран таким, чтобы истинное значение частоты находилось в пределах этой окрестности. Если, например, приближенное значение частоты мы получаем с погрешностью до 10%, то размер окрестности должен составлять не менее 10% от приближенного значения частоты.

Количество эталонных сигналов должно быть увеличено при увеличении возможной ошибки определения приближенного значения частоты с помощью БПФ, т.к. при увеличении ошибки функция коэффициентов кросскорреляции из одноэкстремальной будет превращаться в многоэкстремальную (рис.11.3).

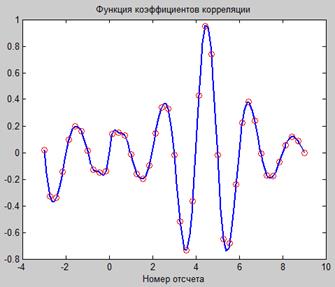
Рис. 11.3. Функция коэффициентов корреляции, полученная в условиях значительного отклонения начального приближения от истинного значения. Истинное значение количества периодов – 4.5, амплитуда сигнала -1.0, СКО нормально распределенного шума – 0.3, начальное приближение количества периодов – 3. Количество эталонных сигналов (и точек аппроксимации) – 21.

Точность определения частоты сигнала будет тем выше, чем ближе начальное приближение к истинной частоте. Поэтому процесс уточнения значения частоты должен быть организован итерационно, на каждом этапе итерации в качестве начального приближения используется уточненное значение частоты, полученное на предыдущем этапе. Размер окрестности на каждом этапе итерации должен сокращаться. В качестве первого приближе­ния берется частота, определенная с помощью БПФ.

Количество итераций для расчета частоты с заданной точностью с помощью описанного способа зависит от того, насколько близко к искомой частоте будет находиться начальное приближение.

Точность определения количества периодов и частоты сигнала описанным выше способом может быть оценена аналитически. Два гармонических сигнала: исходный и эталонный, имеющие частоты f₁ и f₂ или количество периодов n₁ и n₂ , отличающиеся по частоте, можно записать в виде:

x=sin(f₁*t) или sin(2p n₁t/T) = sin(2pn₁fNt/F_sT)=sin(2pn₁i/N)

y=sin(f₂*t) или sin(2p* n₂*t/T)

где T – интервал наблюдения, f-частота отсчетов, N – количество отсчетов, F_s- частота дискретизации.

Коэффициент ковариации сигналов x и y вычисляется по формуле:

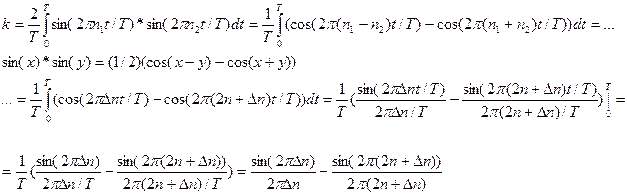
Окончательно

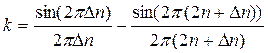
Именно эта функция имеет вид параболы 6 порядка, с вершиной, направленной вверх, если выполнено условие Dn<1/n.

Для нахождения максимума этой функции аналитически нужно продифференцировать ее по Dn и приравнять производную нулю.

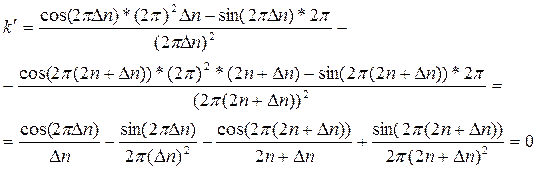
График производной для частного случая, когда количество периодов сигнала равно 10.2, приведено на рис. 11.4.

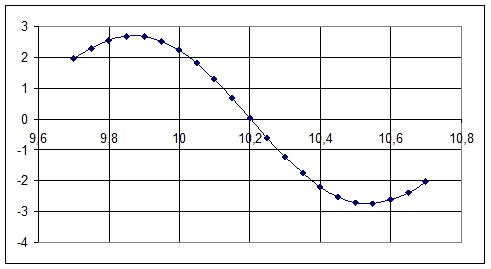
Рис. 11.4. Зависимость производной функции коэффициентов корреляции

от количества периодов сигнала. Точное значение количества периодов – 10,2.

Решение этого уравнения Dn=0 означало бы точное определение количества периодов и частоты с помощью корреляционного сравнения исходного сигнала с эталонами и последующей аппроксимации полученных значений коэффициентов кросскорреляции. При большом количестве периодов решением этого уравнения будет действительно Dn=0, т.к. в этом случае последнее уравнения упрощается и приходит к виду:

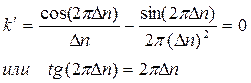
Если же количество периодов мало (например, n<10) и оно не целое, а сигнал зашумлен, то возникает погрешность определения количества периодов, связанная с погрешностью аппроксимации, которая тем не менее будет в несколько раз меньше, чем при использовании БПФ.

Ниже приведен фрагмент программы. Здесь kt - количество отсчетов; kp – количество периодов сигнала; k2 - декремент затухания экспоненциальной огибающей сигнала.

%1. ГЕНЕРАЦИЯ МОДЕЛЬНОГО СИГНАЛА

for i=1:kt %обнуление массива сигнала

y(i)=0;

end

for i=1:kt %генерация модельного сигнала

if(i>0)&(i<=kt/2)

y(i)=sin(2*3.14*kp*i/kt)*i*exp(i/k2)/1200;

end

if(i>kt/2)&(i<(kt))

y(i)=sin(2*3.14*kp*i/kt)*(kt-i)*exp((kt-i)/k2)/1200;

end

y(i)=y(i)+shum*(2*rand(1)-1);

end

%2. ФУНКЦИОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ (БПФ)

bpfy=fft(y,kt);%БПФ

bpf=bpfy.*conj(bpfy)/kt;%БПФ

%нахождение макс. знач. функции БПФ для массива Y

C=max(bpf);

for i=1:kt %поиск количества периодов, соответствующих максимуму БПФ

if (bpf(i)==C)

kpbpf=(i-1);

break

end

end

kp_bpf=kpbpf

%3. СОЗДАНИЕ ЭТАЛОНОВ И КРОССКОРРЕЛЯЦИЯ

fr=kpbpf;

procch=fr/0.8;%область поиска уточненного значения кол-ва периодов относит. kp_bpf

shagkor=fr*procch/3;%шаг поиска

k=0;

for iii=fr-fr*procch:shagkor:fr+fr*procch %цикл для создания 6 эталонов в окрестности приближенного

%значения количества периодов, определенных с помощью БПФ.

k=k+1;

xkor(k)=iii;

kor(k)=0;

for i=1:kt

x(i)=0;

end

%Вычисление массивов эталонных сигналов

for i=1:kt

if(i>0)&(i<=kt/2)

x(i)=sin(2*3.14*iii*i/kt)*i*exp(i/k2)/1200;

end

if(i>kt/2)&(i<(kt))

x(i)=sin(2*3.14*iii*i/kt)*(kt-i)*exp((kt-i)/k2)/1200;

end

end

%вычисление средних значений модельного и эталонных сигналов

x_sr=mean(x);

y_sr=mean(y);

x_sko=0;

y_sko=0;

%вычисление СКО и коэф. корреляции модельного и эталонных сигналов

for i=1:kt

x_sko=x_sko+(x(i)-x_sr)*(x(i)-x_sr);

y_sko=y_sko+(y(i)-y_sr)*(y(i)-y_sr);

kor(k)=kor(k)+(x(i)-x_sr)*(y(i)-y_sr);

end

kor(k)=kor(k)/(sqrt(x_sko*y_sko));

end %конец цикла создания эталонов и вычисления массива коэф. корр.

%СПЛАЙН-АППРОКСИМАЦИЯ И ПЕРЕДИСКРЕТИЗАЦИЯ

xx=1:k;

xi=1:0.1:k;

r1=sin(xx); %только для тестирования сплайн-аппроксимации

yint=interp1(xx,kor,xi,'spline');% сплайн-аппроксимация коэф корреляции

r1=kor;

apr=spaps(xkor,kor,0.000001);

fnplt(apr)

hold on

plot(xkor,r1,'ro')

hold off

%НАХОЖДЕНИЕ УТОЧНЕННОГО ЗНАЧЕНИЯ КОЛИЧЕСТВА ПЕРИОДОВ СИГНАЛА

cmax=max(yint); %нахождение максимума коэф. корр.

for i=1:round((k-1)/0.1+1)

if (yint(i)==cmax)

kp_int=fr-fr*procch+(i-1)*shagkor/10 %уточненное значение частоты по МАХ функции коэф. корр.

end

end

pause;

close all;