ПРИМЕНЕНИЕ ЦОС ДЛЯ ОБРАБОТКИ КОРОТКИХ СИГНАЛОВ. ОКОННАЯ ФИЛЬТРАЦИЯ
Информативным параметром сигнала часто является частота. Для ее определения обычно используется быстрое преобразование Фурье (БПФ). В том случае, если анализируется одночастотный сигнал и он занимает всё временное окно, массив частотного спектра содержит только один ненулевой элемент, номер которого равен количеству периодов сигнала во временном окне (рис. 10.1).
А Б

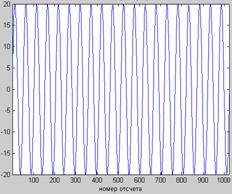
Рис. 10.1.Вил сигнала во временном (А) и частотном (Б) окнах.
Если же сигнал занимает не всё временное окно, а его часть, то частотный спектр будет «растекаться», т.е. будет занимать несколько частотных линий (рис. 10.2).
 А Б
А Б
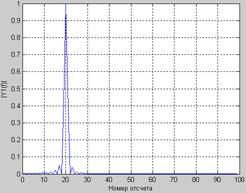
Рис. 10.2
Кроме того, в частотном спектре появляются т.н. боковые лепестки. Этот эффект называют эффектом Гиббса. Количество боковых лепестков видно на рис. 10.3, на котором амплитуда частотной составляющей представлена в логарифмическом масштабе. Количество периодов сигнала здесь равно 50.  Для
Для
подавления боковых лепестков в частотном
спектре применяют оконную фильтрацию.
 В настоящее время известны десятки различных по эффективности весовых функций. В идеальном случае хотелось бы иметь весовую свертывающую функцию с минимальной амплитудой осцилляций, высокую и узкую в главном максимуме.
В настоящее время известны десятки различных по эффективности весовых функций. В идеальном случае хотелось бы иметь весовую свертывающую функцию с минимальной амплитудой осцилляций, высокую и узкую в главном максимуме.
В таблицах 10.1 и 10.2 приведены формулы и основные спектральные характеристики наиболее распространенных и часто используемых весовых окон. Носители весовых функций, в принципе, являются неограниченными и при использовании в качестве весовых окон действуют только в пределах окна и обнуляются за его пределами, что выполняется без дальнейших пояснений. Для упрощения записи формулы приводятся в аналитической, а не в дискретной форме, с временным окном 2t, симметричным относительно нуля (т.е. 0  t). При переходе к дискретной форме окно 2t заменяется окном 2N+1 (полное количество точек дискретизации выделяемой сигнальной функции), а значения t - номерами отсчетов n (t = ntt). Следует заметить, что большинство весовых функций на границах окна (n =
t). При переходе к дискретной форме окно 2t заменяется окном 2N+1 (полное количество точек дискретизации выделяемой сигнальной функции), а значения t - номерами отсчетов n (t = ntt). Следует заметить, что большинство весовых функций на границах окна (n =  N) принимают нулевые или близкие к нулевым значения, т.е. фактическое окно усечения данных занижается на 2 точки. Последнее исключается, если принять 2t = (2N+3) tt.
N) принимают нулевые или близкие к нулевым значения, т.е. фактическое окно усечения данных занижается на 2 точки. Последнее исключается, если принять 2t = (2N+3) tt.
Табл.10.1. Основные весовые функции
| Временное окно | Весовая функция | Фурье-образ |
| Естественное (П) | П(t) = 1, |t|£t; П(t) = 0, |t|>t | П(w) = 2t sinc[wt] |
| Бартлетта (D) | b(t) = 1-|t|/t | B(w) = t sinc2(wt/2). |
| Хеннинга, Ганна | p(t) = 0.5[1+cos(pt/t)] | 0.5П(w)+0.25П(w+p/t)+0.25П(w-p/t) |
| Хемминга | p(t) = 0.54+0.46 cos(pt/t) | 0.54П(w)+0.23П(w+p/t)+0.23П(w-p/t) |
| Карре (2-е окно) | p(t) = b(t) sinc(pt/t) | t·B(w)*П(w), П(w) = 1 при |w|<p/t |
| Лапласа-Гаусса | p(t) = exp[-b2(t/t)2/2] | [(t/b) 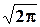 exp(-t2w2/(2b2))] * П(w) exp(-t2w2/(2b2))] * П(w)
|
| Кайзера-Бесселя | p(t) = 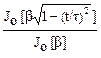 ,
Jo[x] = ,
Jo[x] = 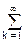 [(x/2)k/k!]2 [(x/2)k/k!]2
| Вычисляется преобразованием Фурье. Jo[x] - модифицированная функция Бесселя нулевого порядка |
 Здесь sinc (от латинского sinus cardinalis – кардинальный синус) – математическая функция. В цифровой обработке сигналов и теории связи нормированная функция sinc обычно определяется как
Здесь sinc (от латинского sinus cardinalis – кардинальный синус) – математическая функция. В цифровой обработке сигналов и теории связи нормированная функция sinc обычно определяется как


Табл.10.2.Характеристики спектров весовых функций
| Параметры | Ед. изм. | П- окно | Барт- летт | Лан-цош | Хен- нинг | Хемминг | Кар- ре | Лаплас | Кайзер |
| Амплитуда: Главный пик 1-й выброс(-) 2-й выброс(+) Ширина Гл. пика Положения: 1-й нуль 1-й выброс 2-й нуль 2-й выброс | t %Гл.п. - “ - wt/2p wt/2p wt/2p wt/2p wt/2p | 0.217 0.128 0.60 0.50 0.72 1.00 1.22 | - 0.047 0.89 1.00 - - 1.44 | 1.18 0.048 0.020 0.87 0.82 1.00 1.29 1.50 | 0.027 0.0084 1.00 1.00 1.19 1.50 1.72 | 1.08 0.0062 0.0016 0.91 1.00 1.09 1.30 1.41 | 0.77 - - 1.12 - - - - | 0.83 0.0016 0.0014 1.12 1.74 1.91 2.10 2.34 | 0.82 .00045 .00028 1.15 1.52 1.59 1.74 1.88 |
В качестве примера на рис. 10.4 приведены результаты применения оконных фильтров Барлетта, Хемминга и Хеннинга.
 А Б
А Б
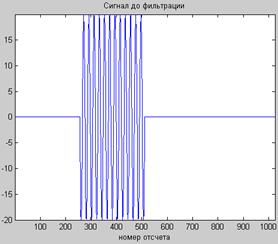
В Г
 |  |
Рис. 10.4. Пример использования оконного фильтра Барлетта.




Рис. 10.5. Пример использования оконного фильтра Хемминга.
 |  |


Рис. 10.6. Пример использования оконного фильтра Хеннинга.
Дата добавления: 2017-01-16; просмотров: 3219;











