ЦИФРОВАЯ ФИЛЬТРАЦИЯ

Цифровая обработка сигналов решает задачи обнаружения и определения параметров информативных сигналов, искаженных шумами и помехами. Для этой цели используются различные средства:

· накопление (временная фильтрация);

· сглаживание (фильтры скользящего среднего и медианные фильтры);

· цифровые частотные фильтры (высокой частоты, низкой частоты, полосовые фильтры);

· оптимальные фильтры (фильтр Колмогорова-Винера, LMS и RLS-фильтры) [2];

· адаптивные фильтры (функцию адаптивных фильтров могут выполнять фильтр Колмогорова-Винера, LMS и RLS-фильтры).

· согласованные фильтры;

· фильтры для борьбы с шумами при нелинейных и нестационарных процессах (фильтр Гильберта-Хуанга)

Выбор способа борьбы с шумами должен производится с учетом свойств и особенностей информативного сигнала и помехи. Чем в большей степени свойства сигнала и шума априори известны, тем может быть получен больший эффект от цифровой обработки. Кроме того, несмотря на обилие стандартных, доведенных до уровня готовых программ цифровой обработки, с учетом конкретных априори известных свойствах информативного сигнала и шума может оказаться полезным разработка новых методов и алгоритмов для борьбы с шумами.

Фильтр скользящего среднего

Пусть мы имеем массив N значений измеренного сигнала, представленный в цифровой форме:

{f₁, f₂, …f_N}, i=1, 2, 3, …N

Для нахождения скользящего среднего в окрестности точки f_i берем среднее арифметическое от K предыдущих и K последующих точек, включая и f_{i .} Таким же образом производим обработку для всех значений i. В результате вычисляем новый массив g_i:

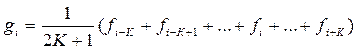
или

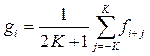
Точки из интервала 2К+1, используемые при вычислении скользящего среднего, могут суммироваться с различными весовыми коэффициентами.

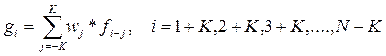
Целесообразность весового суммирования может быть вызвана тем, что, чем ближе суммируемая точка к точке с номером i, тем выше ее значимость, а с ее отдалением влияние ее на точку с номером i yменьшается.

Чтобы не исказить масштаб усредняемой функции, весовые коэффициенты нужно выбирать так, чтобы они удовлетворяли условию:

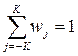
В качестве весовой функции обычно используется функция Гаусса, приведенная на рис. 8.1.

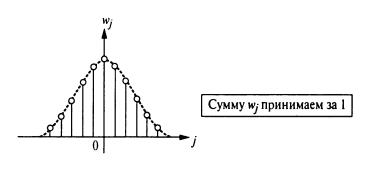
Рис. 8.1. Вид весовой функции Гаусса

Медианный фильтр

В медианном фильтре функция g_i вычисляется по формуле:

g_i = median(x_i-k, x_i-k+1,…, x_i-1, x_i, x_i+1 ,…, x_i+k-1, x_i+k),

где median(z₁, …, z_m, …, z_2k+1) = z_k+1, z_m – элементы вариационного ряда, т.е. ранжированные в порядке возрастания значений z_m: z₁ = min(z₁, z₂,…, z_2k+1) ≤ z₂ ≤ z₃ ≤ … ≤ z_2k+1 = max(z₁, z₂,…, z_2k+1).

Медианная фильтрация более эффективна чем фильтрация на основе скользящего среднего, если входные данные содержат случайные выбросы большой амплитуды.

Цифровой низкочастотный фильтр

Для фильтрации высокочастотного шума может быть применен фильтр низких частот (ФНЧ). Частотная характеристика ФНЧ первого порядка выражается как

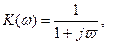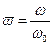где – относительная частота сигнала, 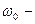частота среза фильтра.

Для фильтрации сигнала нужно вычислить частотный спектр сигнала с помощью преобразования Фурье, затем перемножить частотный спектр сигнала и частотную функцию фильтра и выполнить обратное преобразование Фурье. Второй способ – вычислить импульсную переходную характеристику фильтра (реакцию на единичный импульс), затем выполнить операцию свертки входного сигнала с импульсной переходной характеристикой фильтра.

В программах обработки дискретизированных сигналов, представленных в форме числовых массивов, цикл

for k=1:N

x(k) = A*sin(2*pi*KP1*k/N);

end

создает KP1 периодов дискретизированного синусоидального сигнала в числовом массиве, содержащем N значений. Понятие частоты в этом случае отсутствует и появляется только в том случае, если задать шаг дискретности по времени.

Аналогично этому, в результате выполнения быстрого преобразования Фурье

I=1:N;

X1=fft(x,N);

мы получаем числовой массив X1, который будет содержать N элементов, причем информативной будет только первая половина массива, вторая будет зеркально отображать первую половину. В первой половине массива X1, содержащей N/2 элементов, будет представлен «частотный» спектр. Спектр будет отражать не частоту сигнала, установить которую по числовому массиву, представляющему сигнал во временной области, невозможно, а количество периодов. Т.е. в приведенном выше примере «всплеск» в массиве частотной области будет в элементе с номером KP1. Таким образом, массив частотной области укажет на количество периодов сигнала во временной области.

Частотная характеристика линейного фильтра низких частот может быть вычислена следующим образом:

for i=1:N

H(i)=1/((1+j*i/NC));

end

Здесь NC - полоса пропускания фильтра по уровню 0.7 амплитуды выражена в количестве отчетов спектра БПФ, пропускаемых фильтром. Остальные отсчеты в массиве частотного спектра будут ослабляться по амплитуде. Таким образом понятие постоянной времени фильтра, равно как и полосы пропускания при дискретизированном представлении линейного фильтра отсутствует.

Ниже приведена программа фильтрации сигналов..

%Низкочастотный фильтр

A=1; %амплитуда сигнала

Q=0.1; %амплитуда шума

KP=12;% - количество периодов сигнала

N=1024;%количество точек расчета

NC=12; %NC - полоса пропускания фильтра по уровню 0,7 амплитуды

% выражена в количестве отчетов спектра БПФ, пропускаемых

% фильтром. Остальные отсчеты (в частотном спектре!) будут

% ослабляться по амплитуде

for k=1:N % генерация сигнала и шума

s(k) = A*sin(2*pi*KP1*k/N);

q(k)=Q*(randn(size(N))); %шум

x(k)=s(k)+q(k); % суммирование сигнала и шума

end

for i=1:N

H(i)=1/((1+j*i/NC)); %передаточная функция простого фильтра

%в частотной области

end

i=1:N;

X1=fft(x,N); %частотный спектр сигнала с шумом

Z=ifft(X1.*H); %свертка зашумленного сигнала с частотной

%характеристикой фильтра

На рис. 8.2 приведен пример зашумленного сигнала, его частотного спектра, частотная характеристика фильтра в полулогарифмическом масштабе и сигнал после фильтра.

А Б

В Г

Рис.8.2. Исходный сигнал с шумом (А), его частотный спектр (Б), частотная характеристика фильтра в полулогарифмическом масштабе (В) и сигнал после фильтра (Г).

Низкочастотный фильтр может быть не только первого, но и второго, третьего и т.д. порядка. В общем случае передаточная характеристика фильтра n -го порядка имеет вид:

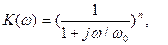где n- порядок фильтра

Недостатком «простого» НЧ-фильтра является наличие амплитудных, частотных и фазовых искажений сигнала в полосе пропускания. Амплитудно-частотная характеристика такого фильтра отличается от идеальной (см. рис. 8.3).

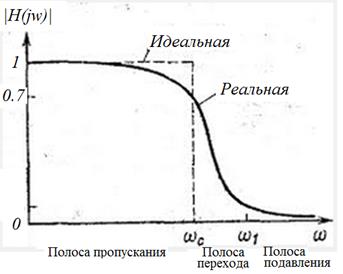
Рис. 8.3. Идеальная и реальная амплитудно-частотные характеристики низкочастотного фильтра.

Более высокое качество фильтрации обеспечивают фильтры Бесселя, Баттерворта, Чебышева.

Фильтр Баттерворта

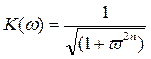
где 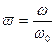- относительная частота среза, 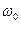- частота среза.

n – порядок фильтра.

Этим обеспечивается масимально плоская АЧХ в полосе пропускания.

Фильтр Чебышева

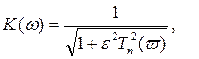- постоянный коэффициент, определяющий степень неравномерности АЧХ в полосе пропускания,

Тn – полином Чебышева 1-го рода n-го порядка.

T₀(x)=1; T₁(x)=x; T₂(x)=2x²-1; T₃(x)=4x³-3x; T₄(x)=8x⁴-8x²+1; T₅(x)=16x⁵-20x³+5x.

Этим обеспечивается максимальное подавление шумов вне полосы пропускания (за счет максимальной крутизны спада АЧХ фильтра) при некоторой, задаваемой коэффициентом 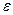, неравномерности АЧХ в полосе пропускания.

Фильтр Чебышева инверсный

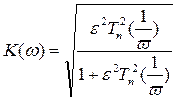
Фильтр Бесселя сконструирован так, чтобы запаздывание сигнала на всех частотах было одинаковым. Т.о. фильтр Бесселя не искажает форму сигнала, спектр которого лежит в полосе пропускания.

Рис. 8.7. ЛФЧХ фильтра Бесселя

Сравнительные характеристики низкочастотных фильтров

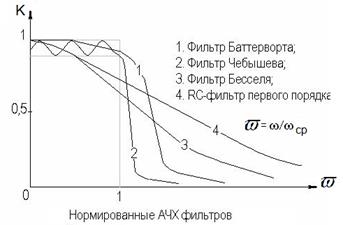
Рис. 8.8. Сравнительные характеристики низкочастотных фильтров

Фильтрация шумов с использованием прямого и обратного БПФ

В том случае, когда частотные спектры сигнала и шума не перекрываются, фильтрация шума может быть произведена путем выполнения БПФ, обнуления спектральных линий шума и последующего обратного БПФ.

A=1;%Амплитуда первого сигнала

B=1; %Амплитуда второго сигнала

Q=0.1;%СКО шума

N=1024;

kp1=50;%количество периодов 1-го сигнала

kp2=120;%количество периодов 2-го сигнала

% Сумма сигналов 1 и 2

for i=1:N

x(i) = A*sin(2*pi*kp1*i/N) + B*sin(2*pi*kp2*i/N);

z(i)=Q*randn(size(N));

y(i) = x(i) + z(i); % Сигнал+шум

end

Y = fft(y,N)/N;%вычисление спектра сигнала с шумом

for i=1:N %"вырезание" спектральных составляющих шума

if (i>125)|(i<40)|((i>55)&(i<110))

Y(i)=0;

end

end

На рис. 8.9 приведен результат работы программы.

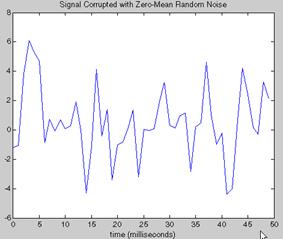
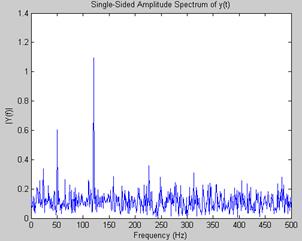
Рис. 8.9. Зашумленный сигнал, представляющий сумму двух синусоидальных сигналов разных частот (содержащих 50 и 120 периодов) (А) и частотный спектр, полученный с помощью БПФ.

Если теперь обнулить участки спектра от 0 до 40, от 55 до 110 и от 125 до 500, а затем выполнить обратное преобразование БПФ (), то получим спектр и сигнал, представленные на рис. 8.10.

А Б

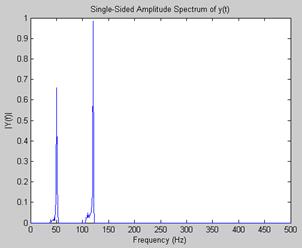
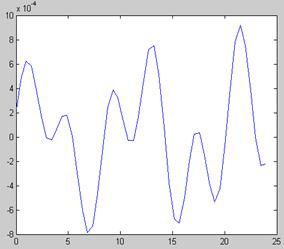
Рис. 8.10. Частотный спектр после удаления спектральных составляющих шума (А) и восстановленный с помощью обратного преобразования Фурье сигнал (Б)

%восстановление исходного сигнала после "вырезания"

%спектральных составляющих шума

z=ifft(Y);