ЛЕКЦИЯ 14 НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ГАЗА

В ПОРИСТОЙ СРЕДЕ

Лейбензон Л. С. получил дифференциальное уравнение для определения давления в пласте при неустановившемся движении в нем идеального газа.

Для его получения при изотермической фильтрации использовано уравнение состояния идеального газа:

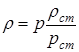. (14.1)

Потенциальная функция имеет вид:

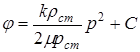. (14.2)

Обозначив р²=Р и проделав преобразования общего уравнения нестационарной фильтрации, он получил:

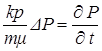. (14.3)

По внешнему виду уравнение (14.3) не отличается от уравнения пьезопроводности, но множитель перед лапласианом переменен. В связи с этим уравнение (14.3) нелинейно в отличие от линейного уравнения пьезопроводности . Решается уравнение (14.3), как правило, приближенно.

Для получения приближенного решения используется метод линеаризации, а именно, переменное давление р перед лапласианом заменяется на некоторое постоянное. Лейбензон Л. предложил замену на р_к (начальное давление в пласте); Чарный И.– на р_ср = р_min+0,7(p_max - p_min), где p_max и p_min– максимальное и минимальное давление в пласте за расчетный период.

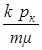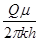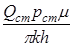При указанных допущениях решение будет иметь такой же вид, что и в случае упругой жидкости, но при этом в данных решениях давлению р будет соответствовать Р = р², k –Þ k^/ = , Þ . Таким образом, изменение давления при нестационарной фильтрации газа описывается соотношением:

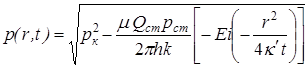. (14.4)

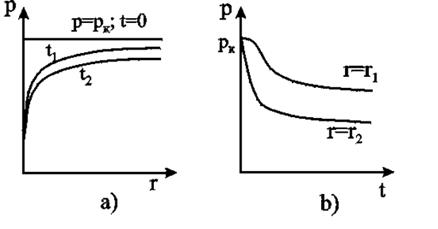
Рисунок 14.1 – Кривые распределения давления по пласту при неустановившемся притоке газа к скважине в разные моменты времени (а) и изменение давления с течением времени в фиксированных точках пласта (b)

При малых значениях r²/(4k^/t) можно заменить интегрально-показательную функцию логарифмической:

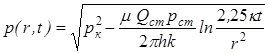. (14.5)

Формулы (14.4), (14.5) определяют при фиксированных значениях времени распределение давления вокруг газовой скважины, работающей с постоянным дебитом с момента t = 0. Если задать значение r, то можно найти изменение давления в данной точке с течением времени (рисунок14.1b). В частности, можно найти давление на забое (при r = r_c) после начала работы скважины.