Координатне подання векторного добутку.
З’ясуємо, як обчислити координати векторного добутку, якщо відомі координати векторів-множників. Для цього ми використаємо розкладання векторів-множників за одиничним базисом простору.
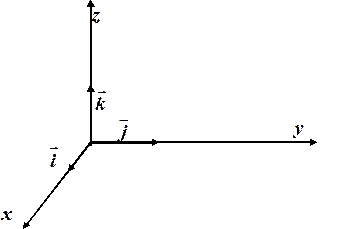
Нехай вектори 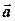 і
і 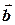 задані своїми координатами:
задані своїми координатами:
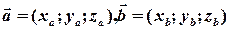 .
.
Розкладемо вектори 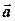 і
і 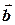 за одиничним декартовим базисом
за одиничним декартовим базисом 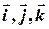 :
:
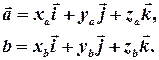
Тоді
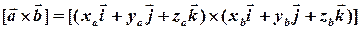 .
.
Використовуючи алгебраїчні властивості векторного добутку ми можемо, обчислюючи векторний добуток двох сум, перемножувати доданки почленно:
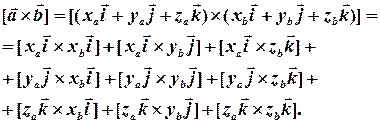
Як ми вже знаємо, векторний добуток колінеарних векторів рівний нулю. Так само рівний нулю й векторний добуток однакових множників: 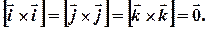 Це спрощує вираз для
Це спрощує вираз для 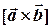 , зменшуючи кількість доданків до шести:
, зменшуючи кількість доданків до шести:
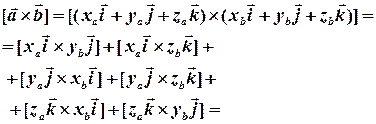
користуючись властивостями однорідності та антикомутативності векторного добутку, здійснюємо подальше спрощення виразу:
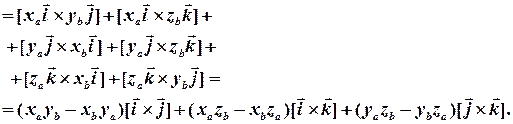
Для отримання остаточного вигляду розглядуваного виразу залишилось з’ясувати, чому дорівнюють векторні добутки відповідних пар базисних векторів: 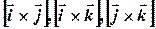 . Розглянемо векторний добуток
. Розглянемо векторний добуток 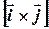 . Модуль вектора
. Модуль вектора 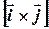 дорівнює площі паралелограма, побудованого на векторах
дорівнює площі паралелограма, побудованого на векторах 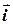 та
та 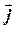 . Цей паралелограм є квадратом зі стороною, рівною одиниці, отже його площа рівна одиниці. Таким чином,
. Цей паралелограм є квадратом зі стороною, рівною одиниці, отже його площа рівна одиниці. Таким чином, 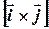 є одиничний вектор. Беручи до уваги, що вектор
є одиничний вектор. Беручи до уваги, що вектор 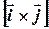 повинен бути перпендикулярним до векторів
повинен бути перпендикулярним до векторів 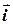 та
та 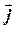 і напрямленим згідно правилу правої руки (якщо вектори
і напрямленим згідно правилу правої руки (якщо вектори 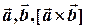 зведені до спільного початку, то вектор
зведені до спільного початку, то вектор 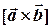 повинен бути направлений так, як направлений середній палець правої руки, великий палець якої направлений по першому співмножнику (тобто по вектору
повинен бути направлений так, як направлений середній палець правої руки, великий палець якої направлений по першому співмножнику (тобто по вектору 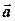 ), а вказівний— по другому (тобто по вектору
), а вказівний— по другому (тобто по вектору 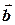 )), легко зрозуміти, що він співпадає з третім базисним вектором
)), легко зрозуміти, що він співпадає з третім базисним вектором 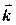 , тобто
, тобто 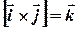 . Міркуючи аналогічно, отримаємо:
. Міркуючи аналогічно, отримаємо: 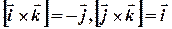 .
.
Отже, остаточно,
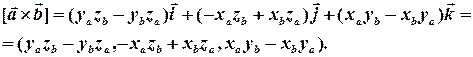
Дата добавления: 2021-05-28; просмотров: 604;











