Координатне подання векторного добутку в детермінантній формі.
Для отримання формули обчислення координат векторного добутку через координати векторів-множників використаємо поняття визначника (або детермінанта) другого порядку (див.§2). Згадаємо: визначник другого порядку – це визначник квадратної матриці  , позначається
, позначається 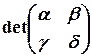 або
або  , –це число, яке обчислюється за формулою:
, –це число, яке обчислюється за формулою:
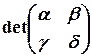 =
= 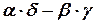 .
.
Теорема (про координатне подання векторного добутку в детермінантній формі). Якщо вектори 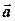 і
і 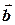 задані своїми координатами:
задані своїми координатами:
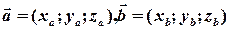 ,
,
то векторний добуток векторів 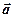 і
і  визначається формулою:
визначається формулою:
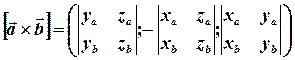 .
.
Доведення очевидне.
Зауваження. Для зручності обчислення векторного добутку корисно координати заданих векторів записати спочатку у вигляді наступної таблиці:
 .
.
Закриваючи тут спочатку перший стовпчик, потім другий і третій, ми отримаємо послідовно три визначника другого порядку; обчислюючи їх і взявши другий зі знаком мінус, ми таким чином знайдемо три координати векторного добутку 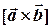 .
.
Формулі обчислення координат векторного добутку за координатами векторів-множників можна надати ще більш компактного вигляду:
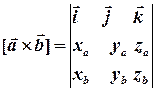 .
.
Дійсно, якщо розгорнути цей визначник (див. §9) за елементами першого рядка, то отримаємо попередню формулу.
Приклад.
Дано 2 вектори  і
і  . Знайти координати векторного добутку
. Знайти координати векторного добутку 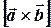 .
.
Розв’язання. Складаємо таблицю:
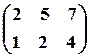 .
.
Закриваючи послідовно стовпчики цієї таблиці, ми отримаємо три визначники другого порядку, обчислюючи їх і, взявши другий зі знаком мінус, знайдемо шукані проекції:

Дата добавления: 2021-05-28; просмотров: 688;











