Радианная мера угла.

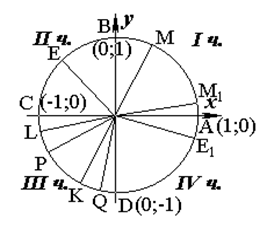
Отметим на оси Ох от начала координат точку А и проведем через нее окружность с центром в точке О. Радиус ОА будем называть начальным радиусом.

Угол Р (ОМ; ОЕ) можно описать как получившийся в результате вращения вокруг начала координат луча с началом в точке О от положения ОМ - начального до положения ОЕ - конечного. Это вращение может происходить или против часовой стрелки или по часовой стрелке, причем

а) либо на неполный оборот,

б) либо на целое число полных оборотов;

в) либо на целое число полных оборотов и неполный оборот.

Меры углов, ориентированных против часовой стрелки, считаются положительными, а по часовой стрелки - отрицательными

Будем считать равными углами такие углы, для которых при совмещении каким либо образом их начальных лучей совмещаются и конечные лучи, причем движение от начального луча к конечному осуществляется в одну и ту же сторону на одно и то же количество полных и неполных оборотов вокруг точки О.

Нулевые углы считаются равными.

Свойства мер углов:

Существует угол, мера которого равна 1 - единица измерения углов. Равные углы имеют равные меры. Мера суммы двух углов равна сумме мер углов. Мера нулевого угла равна нулю.

Наиболее распространенные меры углов - градусная и радианная.

Единицей измерения углов в градусной мере является угол величины в один градус - 1/180 часть развернутого угла.

В качестве окружности с центром в начале координат мы будем брать окружность единичного радиуса, обозначая точки ее пересечения с координатными осями A(1;0), B(0;1), C(-1;0), D(0;-1). В качестве начального угла у рассматриваемых углов будет браться луч ОА.

Координатные оси абсцисс и ординат взаимно перпендикулярны и разбивают плоскость на четыре координатные четверти: I, II, III, IV (см. рисунок).

В зависимости от того, в какой координатной четверти окажется радиус ОМ, угол α будет так же углом этой четверти.

Так, если 00<α<900 , то угол α – угол первой четверти;

Если 900<α<1800 , то угол α – угол второй четверти;

Если 1800<α<2700 , то угол α – угол третьей четверти;

Если 2700<α<3600 , то угол α – угол четвертой четверти.

Очевидно, что при прибавлении к углу целого числа оборотов получается угол той же четверти.

Например, угол 4300 является углом I – ой четверти, так как 4300 = 3600 + 700 = 700;

Угол 9200 является углом III-ей четверти, так как 9200 = 3600 ·2 + 2000 = 2000

(т. е. число целых оборотов можно не учитывать!)

Углы 00, ± 900 , ± 1800, ± 2700, ± 3600 – не относятся ни к какой четверти.

Давайте определим, углом какой четверти является угол α, если:

α =2830 (IV) α = 1900 (III) α =1000 (II) α = -200 (IVч –отрицательное направление)

B курсе геометрии были определены синус, косинус, тангенс и котангенс угла α при 00 ≤ α ≤ 1800 . Теперь мы рассмотрим эти определения на случай произвольного угла α.

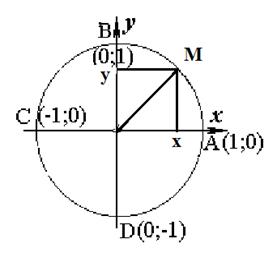
Пусть при повороте около точки О на угол α начальный радиус ОА переходит в радиус ОМ.

Синусом угла α называется отношение ординаты точки М к длине радиуса, т. е.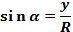

Косинусом угла α называется отношение абсциссы точки М к длине радиуса, т. е.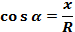

Тангенсом угла α называется отношение ординаты точки М к ее абсциссе, т. е.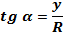

Котангенсом угла α называется отношение абсциссы точки М к ее ординате, т. е.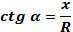

Рассмотрим примеры вычисления тригонометрических функций с помощью таблиц значений некоторых углов. Прочерки сделаны в том случае, когда выражение не имеет смысла.

α (град)
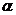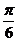
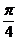
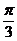
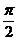
(рад)						π		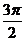2π
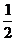
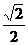
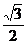
sin α							-1
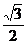
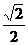
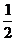
cos α						-1
tg α					-		-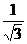
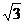
ctg α	-					-		-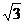

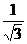
Пример №1.Найти sin300; cos450; tg600.

Решение: а) находим в столбике таблицы sinα и в строчке 300, на пересечении столбца и строчки находим значение sin 300- это число 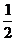. Пишут так: sin 300 =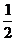

б) находим в столбике таблицы cosα и в строчке 450, на пересечении столбца и строчки находим значение cos 450 - это число 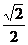. Пишут так: cos 450 =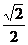

в) находим в столбике таблицы tgα и в строчке 600, на пересечении столбца и строчки находим значение tg 600- это число 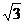. Пишут так: tg 600 = .

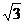Пример №2

Вычислитьа) 2сos 600 + 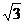cos 300 = 2·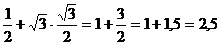

б)3tg 450 ·tg 600 = 3·1· 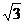= 3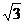

Вычислите самостоятельно: а) 5sin 300 - ctg 450 б) 2sin 300 + 6cos 600 – 4tg 450

в) 4tg 600·sin 600 в) 2cossin 900 + 5tg 1800