В качестве примера на этом рисунке рассмотрена статическая ВАХ силового диода, работающего в динамическом режиме.
В зависимости от величины угла отсечки различают следующие режимы работы НЭ, а соответственно и радиотехнических устройств:
- класс А при  =
=  (режим без отсечки тока);
(режим без отсечки тока);
- класс АВ при  /2<
/2<  <
<  ;
;
- класс В при  =
=  /2;
/2;
- класс С при  <
<  /2.
/2.
Как уже отмечалось, ток, протекающий через НЭ в режиме с отсечкой тока, представляет собой периодическую последовательность импульсов, которую можно разложить в ряд Фурье с учетом четности функции косинуса. Частота первой гармоники считается основной, именно она входит в аргумент рис.3.4.
Аналитическое выражение тока имеет вид:
i = S(u0-Umaxcos 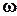 t - E
t - E  ). (3.3)
). (3.3)
При 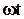 =
=  , ток равен нулю i =0 и получаем выражение:
, ток равен нулю i =0 и получаем выражение:
0 = S(u0-Umaxcos  - E
- E  ). (3.4)
). (3.4)
Вычитая (3.3.) из (3.4.), получим:
i = SUmax(сos 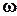 t - cos
t - cos  ). (3.5)
). (3.5)
При 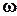 t =0 ток принимает максимальное значение.
t =0 ток принимает максимальное значение.
Imax = SUmax(1 - cos  ). (3.6)
). (3.6)
Эти формулы используют для определения амплитуд гармоник по методу угла отсечки.
Разложим в ряд Фурье (3.5):
Imax.1 = 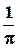
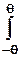 i(t)cos
i(t)cos 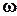 t d(
t d( 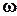 t) =
t) =
= 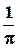
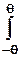 S Umax (cos
S Umax (cos  t.- cos
t.- cos  ) cos
) cos  t d(
t d(  t) =
t) =
= S Umax 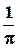 (
( 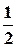
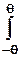 d(
d( 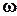 t) +
t) + 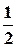
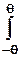 cos 2
cos 2 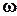 t d(
t d( 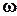 t) -
t) -
- cos 
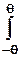 cos
cos 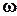 t d(
t d( 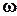 t) = S Umax
t) = S Umax 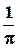 (
(  - sin
- sin  cos
cos  ). (3.7)
). (3.7)
Отношение амплитуды первой гармоники к максимальной:
 1= Imax.1/Imax =
1= Imax.1/Imax = 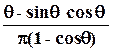 . (3.8)
. (3.8)
Это выражение зависит только от угла отсечки и обозначается 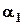 (
(  ).
).
Аналогично составим отношения для других составляющих выходного тока:
 0 = I0/Imax =
0 = I0/Imax = 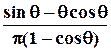 ; (3.9)
; (3.9)
 2= Imax.2/Imax =
2= Imax.2/Imax = 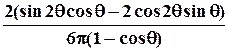 . (3.10)
. (3.10)
Отношение амплитуды любой гармоники (k>2) к максимальной:
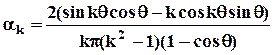 . (3.11)
. (3.11)
Коэффициенты (3.11) называются коэффициентами разложения косинусоидального импульса (коэффициенты Берга). Они рассчитаны и сведены в таблицы или определяются по специальным графикам, показанным на рис.3.5.
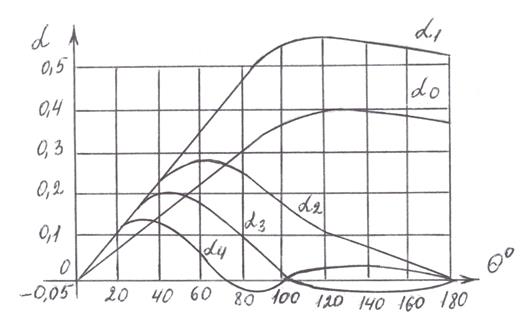
Рис.3.5. Коэффициенты Берга.
Из графика видно, что амплитуды гармоник максимальны при вполне определенных (оптимальных) углах отсечки:
 k.опт=
k.опт= 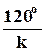 ,
,
где k – номер гармоники.
Из рис.3.5 видно, что Imax.1 максимальна при 1200, Imax.2 максимальна при 600, Imax.3 максимальна при 400 и т.д.
Таким образом, выбирая режим работы НЭ можно обеспечить в выходном токе максимальную амплитуду той или иной гармоники.
Расчет работы диода производится в следующем порядке.
1) По известным E  , u0 , Umax находят угол отсечки
, u0 , Umax находят угол отсечки  по (3.2).
по (3.2).
cos  =
= 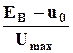 , откуда
, откуда  = arc cos
= arc cos 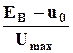 .
.
2) По формуле (3.7) Imax = S Umax 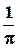 (
(  - sin
- sin  cos
cos  ) и по графику
) и по графику
характеристики (рис.3.4) определяется максимум выходного тока сигнала.
3) По таблицам или графику (рис.3.5) находятся коэффициенты Берга
для соответствующего угла отсечки.
4) Амплитуда любой гармоники определяется по формуле
Imax.k=  k Imax. (3.12)
k Imax. (3.12)
Следует отметить, что расчет выходного тока транзистора методом угла отсечки несколько отличается от вышеприведенного расчета диода. Причина в инерционности процесса протекания тока в транзисторе: на протяжении периода переменного воздействия в базе БТ происходит накопление и рассасывание электрического заряда. Поэтому угол отсечки коллекторного тока в области высоких частот  ВЧ не равен углу отсечки по входной цепи
ВЧ не равен углу отсечки по входной цепи  ВХ. Рассмотрение динамического режима большого сигнала для БТ позволяет аппроксимировать график функции зависимости заряда в базе от времени Q(
ВХ. Рассмотрение динамического режима большого сигнала для БТ позволяет аппроксимировать график функции зависимости заряда в базе от времени Q(  t) в виде синусоидального импульса с амплитудой Imax и углом отсечки
t) в виде синусоидального импульса с амплитудой Imax и углом отсечки 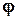 ВЧ. Расчетные формулы, в этом случае принимают вид:
ВЧ. Расчетные формулы, в этом случае принимают вид:
 ВЧ =
ВЧ =  .
.
И вычисление амплитуды гармоник тока коллектора производится по следующим формулам:
IК0 =  0 (
0 (  ВЧ) IК.max.
ВЧ) IК.max.
IКmax1 =  1 (
1 (  ВЧ) IК.max.
ВЧ) IК.max.
В общем виде:
IКmaxk =  k (
k (  ВЧ) IК.max.
ВЧ) IК.max.
ВЫВОДЫ:
1. Расчет динамического режима методом угла отсечки нашел ши-
рокое применение благодаря простоте расчета и достаточной точности.
2. Расчет проводится с помощью статической ВАХ , динамической
(средней) крутизны, угла отсечки и коэффициентов Берга.
3. При рассчете цепей с биполярным транзистором учитывается инерционность протекания тока и накопление электрического заряда в базе.
ЗАКЛЮЧЕНИЕ
В этой части пособия было показано, что полное представление о нелинейной цепи складывается из рассмотрения нелинейных свойств её отдельных элементов. Выяснено, при каких условиях работы того или иного электронного элемента можно применять линейные методы расчета параметров цепи, и в каких случаях необходимо пользоваться положениями нелинейной теории. Строго говоря, все элементы нелинейны, и выбор метода расчета во многом зависит от требуемой точности определения параметров. Основными параметрами являются статические, средние и динамические параметры: крутизна, проводимость и сопротивление. Эти параметры можно определить по известным вольт-амперным характеристикам. Вычисления осуществляются графическими и аналитическими методами. В отличие от линейных цепей, исходные нелинейные уравнения не могут быть решены точно, а лишь приближенно. Графические методы отличаются простотой, но требуют графического изображения характеристик и воздействия. Их недостатком является малая точность, а достоинством экспрессность. Аналитические методы предпочтительны в тех случаях, когда требуется более высокая точность, получение решения задачи в общем виде и при задании характеристик и воздействия в виде формул. Аналитические методы позволяют программированное выполнение вычислений, что находит широкое применение благодаря экономии времени. На практике для аналитических методов расчета применяют различные виды аппроксимации вольт-амперных характеристик, особенно часто используют аппроксимацию полиномом первой, второй и третьей степени. Воздействие представляется суммой двух составляющих: постоянной и гармонической. Полином первой степени позволяет определить параметры элемента в режиме слабого воздействия, при котором амплитуда переменной составляющей мала по сравнению со смещением. Полином второй степени описывает начальный участок ВАХ, а полином третьей степени необходим для расчета верхнего загиба ВАХ силовых диодов, транзисторов и ламп, а также для полной аппроксимации ВАХ тунельного диода. Расчет динамических режимов работы НЭ в условиях сильного сигнала производится графо-аналитическими методами трех, пяти ординат и методом угла отсечки. Эти методы относятся к гармоническому анализу, который позволяет определить амплитуды гармоник, появившихся на выходе цепи, т.е являющихся реакцией нелинейного элемента. На основании проведенного анализа можно сделать вывод, что номер высшей гармоники совпадает с высшей степенью аппроксимирующего полинома. Все методы расчета, рассмотренные в этой части пособия, будут в дальнейшем применены к сложным цепям.
ЛИТЕРАТУРА
Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. - 512 с.
Конторович М.И. Нелинейные колебания в радиотехнике (автоколебательные системы). – М.: Советское радио, 1973. – 320 с.
Мейке М., Гудлах Ф. Радиотехнический справочник. Том 2. Перевод с немецкого. - М.-Л.: Госэнергоиздат, 1962. - 576 с.
Фролкин В.Т., Попов Л.Н. Импульсные и цифровые устройства. – М.: Радио и связь, 1992. – 336 с.
Шинаков Ю.С., Колодяжный Ю.М. Основы радиотехники. – М.: Радио и связь, 1983. – 320 с.
Дата добавления: 2018-05-10; просмотров: 1669;











