Разностные уравнения.

В качестве аналогов дифференциальных уравнений можно рассматривать разностные уравнения (уравнения в конечных разностях)

При использовании прямых разностей неоднородные линейные разностные уравнения имеют вид:

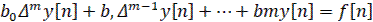, (6)

где 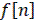– заданная, а 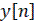- искомая решетчатая функция. При 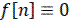уравнение (6) становится однородным разностным уравнением, решением которого будет .

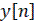Разностное уравнение (6) может быть записано в другом виде

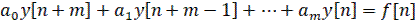(7)

Коэффициенты этого уравнения определяются из зависимости

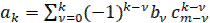(8)

где биноминальные коэффициенты

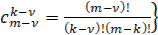(9)

При использовании обратных разностей уравнение в конечных разностях будет

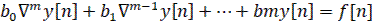(10)

или

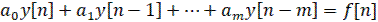(11)

Коэффициенты последнего уравнения определяются вложениями

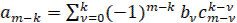(12)

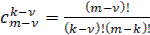(13)

Разностные уравнения можно рассматривать как рекурентные соотношения, позволяющие вычислить значения 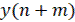при n=0,1,2,… для заданных начальных значений 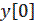, , 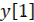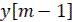и уравнения вида (7) при значении 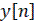при n=0,1,2,… для заданных начальных значений 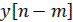, ,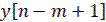…, 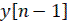и уравнения вида (11). Также вычисления вечно минимизируются, а так же не представляют никаких принципиальных трудностей и при ручном счете даже в случае, когда коэффициенты разностных уравнений 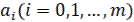с течением времени и заменяются. Это отличает разностные уравнения от их непрерывных аналогов – дифференциальных уравнений.

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

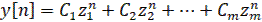(14)

где 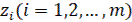– корни характеристического уравнения

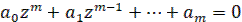(15)

и 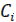– произвольные постоянные

Условие устойчивости: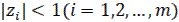

Для исследования решений разностных уравнений в общем виде широко используются дискретные преобразования Лапласа, z – преобразование, 𝛚 – преобразование, а так же частотные методы.