Решетчатые функции.

Введем понятие решетчатой функции времени f [nT] или в сокращенной записи f[n], значения которой определены в дискретные моменты времени

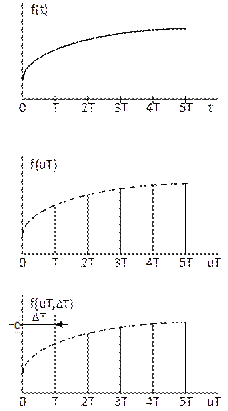
Рисунок 5.

T=nT, где n – целое число, а Т – период повторения. Операция замены непрерывной функции решетчатой

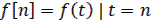(1)

Показана на рисунке 5.

Изображение на рисунке 5 (б) ординаты представляют собой так называемые дискреты исходной непрерывной функции f(t) при t=nT (рисунок 5). Дискреты f(t) могут быть определены для смещения моментов времени t=nT+ΔT=(n+Ԑ)T. Смещение ΔT=const могут быть положительной или отрицательной величиной при выполнении условия |ΔT|˂T.

Относительное смещение 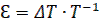по модулю меньше единицы.

Образование смещенной решетчатой функции f[nT, ΔT], как в сокращенной записи f[n,Ԑ], из непрерывной функции f(t) для случая ΔT˃0 изображено на рисунке 5(в). В последующем будем считать n≥0 и Ԑ˃0. В случае необходимости рассмотрения функции f(n,Ԑ) с отрицательным параметром Ԑ˂0 дискретное время можно представить в виде 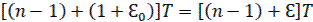. Тогда решетчатая функция может быть записана в виде f[n-1,Ԑ], где .

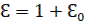Введем понятие основной огибающей функции. Под основной огибающей будем понимать непрерывную функцию, совпадающую с заданными дискретами, которая может быть получена как результат решения дифференциального уравнения, порядок которого наименьший по сравнению с другими возможными огибающими, а для периодических решетчатых функций, кроме того выполняется требование минимальности значений частот гармоник. Так, например решетчатой функции 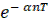могут соответствовать огибающие 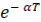и 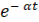( 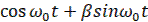), где 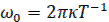, 𝛋 – целое число, 𝛃 – любое число. Однако первая из них (основная огибающая) может быть получена в результате решения дифференциального уравнения первого порядка, тогда как вторая в результате решения дифференциального уравнения второго порядка.

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность

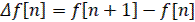(2)

либо первая обратная разность

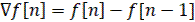(3)

Обе эти разности показаны на рисунке 6

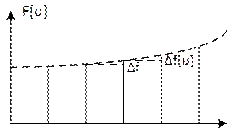
Рисунок 6.

Разновидности могут быть определены и для смещенных решетчатых функций .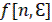

Вследствие идентичности формул для Ԑ≠0 и Ԑ=0 принято, что Ԑ=0.

Прямая разность определяется в момент времени 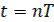по будущему значению решетчатой функции при 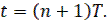Это можно сделать в тех случаях, когда будущее значение известно.

Обратная разность определяется для момента времени 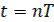по прошлому значению решетчатой функции в момент времени .

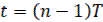Аналогом второй производной непрерывной функции для решетчатой функции служат вторые разности: прямая

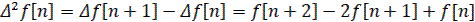(4)

и обратная

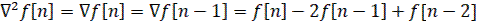(5)

Обратные разности обладают важной особенностью. Если решетчатая функция определена только для положительных значений аргумента, т.е. 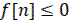при n˂0, то в (1) n=0 прямая разность 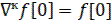для любого целого положительного 𝛋.