Свойства несмещенных решетчатых функций.
1) Свойства линейности
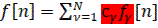 (33)
(33)
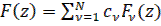 (34)
(34)
2) Теорема запаздывания и упреждения
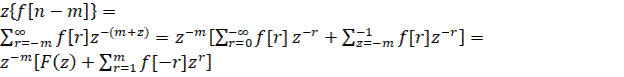 (35)
(35)
3) Теорема умножения оригинала на экспоненту
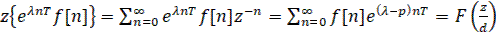 ;
;
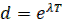 . (35)
. (35)
Для смещенной решетчатой функции
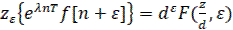 (36)
(36)
4) Теорема об умножении оригинала на смешенную функцию
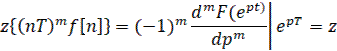
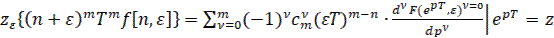 (37)
(37)
5) Изображение разностей
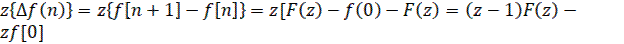 (38)
(38)
Для первой обратной разности можно найти
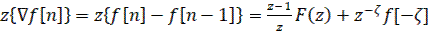 (39)
(39)
Если для отрицательных аргументов решетчатая функция тождественно равна нулю, то (39) упрощается
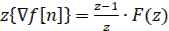 (40)
(40)
Для кратной обратной разности при 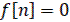 для
для 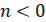
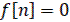 для
для 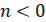
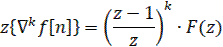
6) Изображение сумм
Изображение полной суммы
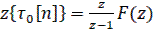 (41)
(41)
Для случая к-кратного суммирования
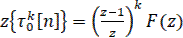 (42)
(42)
Или
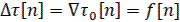 (43)
(43)
Т. е., взятие прямой разности и взятие неполной суммы (или обратной разности и полной суммы) решетчатой функции являются обратными операциями.
7) Изображение решетчатых функций с изменяемым периодом следования
Период чередования 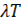 при
при 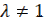 .
.
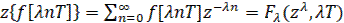 (43)
(43)
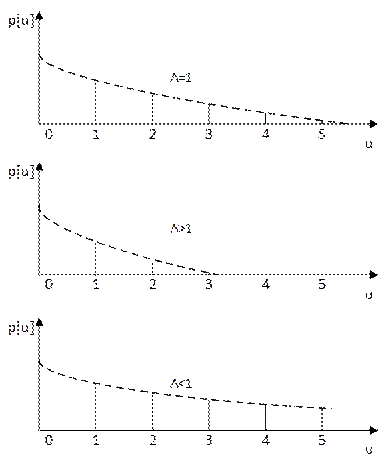
8) Сумма ординат решетчатых функций
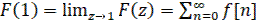 (44)
(44)
9) Конечное значение решетчатой функции
имеем:
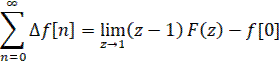
Кроме того, можно записать
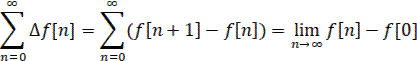
Следовательно:
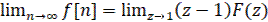 (45)
(45)
Для первой обратной разности
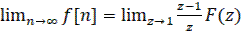 (46)
(46)
10) Начальное значение решетчатой функции
Конечное и начальное значение непрерывной функции 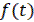 :
:
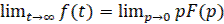 ;
;
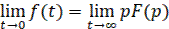
11) Свертка решетчатых функций
Если 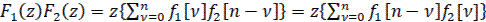
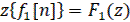
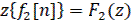
13.2.Нелинейные САР
Нелинейной САР называется система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением.
Виды нелинейных звеньев:
1. Звено линейного типа
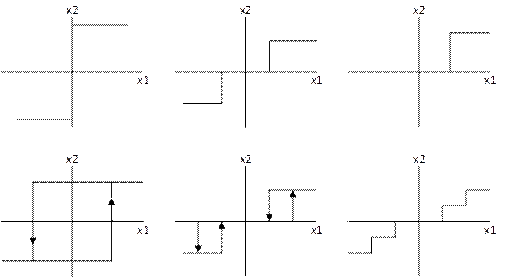
2. Звено с кусочно-линейной характеристикой
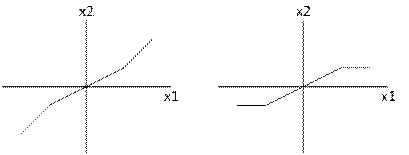
3. Звено с криволинейной характеристикой любого очертания
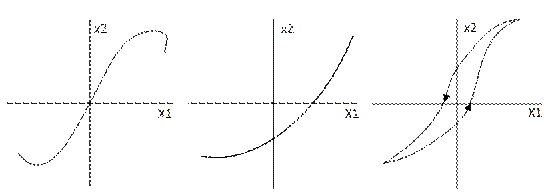
4. Звено, уравнение которого содержит произведения переменных как их производных и другие их комбинации
5. Нелинейное звено с запаздыванием
6. Нелинейное импульсное звено
7. Логическое звено
8. Звенья, описываемые кусочно-линейными дифференциальными уравнениями
Различают статические и динамические нелинейности которыми соответственно являются нелинейности статических характеристик, а второе в виде нелинейных дифференциальных уравнений.
Общий метод составления уравнений для нелинейных систем состоит в следующем. Сначала производится линеаризация уравнений всех звеньев системы, для которых это допустимо, кроме существенно нелинейных звеньев. Затем составляются уравнения этих последних звеньев со всеми допустимыми упрощениями их характеристик.
Разделим все нелинейные системы на два больших класса.
1) К первому классу Н.С. отнесем такие, в которых уравнение нелинейного звена приводится к любому их виду, т.е. когда над знаком нелинейности стоит только выходная величина (и ее производные), либо только выходная величина (и ее производные). Причем вся схема может быть приведена к системе с одним нелинейным знаком
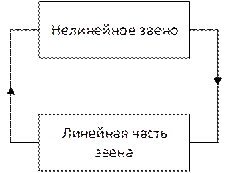
2) Второй класс Н.С. включает в себя системы с любым числом нелинейных звеньев, когда под знаки нелинейных функций входят различные переменные, связанные между собой линейной передаточной функцией.
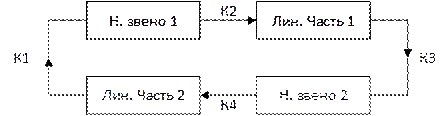
Процессы в Н.С.АР имеют ряд существенных особенностей, которые не встречаются в линейных системах.
В общем случае на плоскости параметров системы может быть не два вида областей (устойчивая и неустойчивая), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением регулируемой величины; 2) область устойчивых автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям.
Если процессы в системе имеют вид
а)
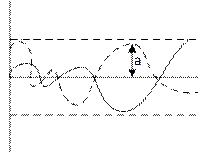
то рановесное состояние х=0, неустойчиво.
б)
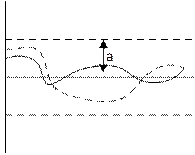
в)
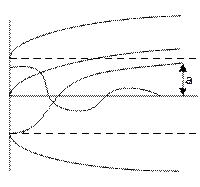
В том случае оба указательных на рис
а) колебания в периодных процессах стремятся к одной и той же амплитуде, к одной и той же амплитуде, к одной и тоже частоте, система будет обладать устойчивыми автоколебаниями с амплитудой «а».
На рис. б) и в) показаны случаи, когда равновесное состояние (х=0) системы устойчиво в «малом», т.е. при начальных условиях, не выводящих отклонения в периодном процессе за определенную величину «а», и неустойчивую в «большом», т.е. при начальных условиях, выводящих отклонение в переходном процессе за пределы величины «а». Здесь граничным процессом является неусточивый периодический процесс собственного движения системы с амплитудой «а» (переходный процесс расходится от него в обе стороны).
Пример. Переходный процесс и автоколебания в релейной системе автоматического регулирования.
Пусть система описывается уравнением вида
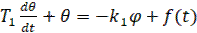 (*)
(*)
где θ – температура, φ – отключение регулирующего органа, f(t) – внешние воздействия. При отклонении температуры θ появляется ток в диагонали моста того или иного направления и замыкается тот или иной контакт реле, включающий напряжение в той или иной обмотке возбуждения электродвигателя.
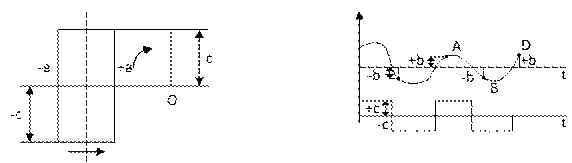
Считаем что ток пропорционален отклонению температуры объекта θ, а скорость 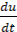 отклонения регулирующего органа пропорциональна напряжению на обмотках возбуждения электродвигателя, можно в данном случае считать выходной величиной т.е.
отклонения регулирующего органа пропорциональна напряжению на обмотках возбуждения электродвигателя, можно в данном случае считать выходной величиной т.е. 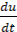 , а входной – θ.
, а входной – θ.
Следовательно, уравнение регулятора записывается следующим образом
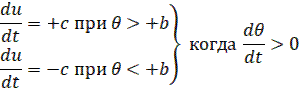

Рассмотрим два произвольных участка переходного процесса (при f(t)=0) в данной системе (AB и BD).
На участке АВ уравнение регулятора будет 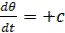 . Дифференцируя (f) по t и подставляя туда +с, получаем при f(t)=0 следующее уравнение системы регулирования на участке АВ
. Дифференцируя (f) по t и подставляя туда +с, получаем при f(t)=0 следующее уравнение системы регулирования на участке АВ
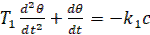 (2)
(2)
На участке BD
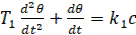 (3)
(3)
Решением уравнения (2) будет
 (4)
(4)
откуда получаем
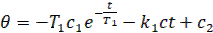 (5)
(5)
Если отсчитывать время t от начала участка АВ, то начальные условия будут
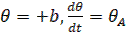 ; при t=0
; при t=0
где 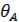 – пока неизвестно. Используя начальные условия находим произвольные постоянные для уравнения (5).
– пока неизвестно. Используя начальные условия находим произвольные постоянные для уравнения (5).
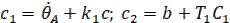
Для участка BD, отсчитывая время t от начала этого участка, получим решение
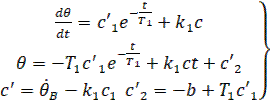 (7)
(7)
Все остальные участки кривой переходного процесса будут определяться, очевидно, такими же решениями, но только с другими числовыми значениями 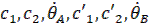 . Величины
. Величины 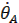 и
и 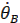 необходимы для определения произвольных постоянных.
необходимы для определения произвольных постоянных.
Выясним теперь, возможны ли автоколебания в этой системе, т.е. устойчивое ли периодическое решение. Для этого нужно, очевидно, чтобы в конце D одного периода колебаний получались такие же θ и 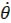 , какие были в начале его А.
, какие были в начале его А.
Отметим, что оба полупериода (AB и BD) должны быть одинаковыми вследствие симметрии характеристики
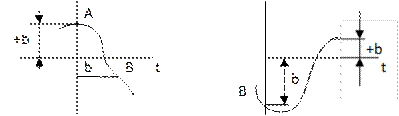
Поэтому для определения автоколебаний достаточно рассмотреть участок АВ и потребовать, чтобы
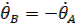 (8)
(8)
Обозначив период искомых автоколебаний через 2Т, а длительность участка АВ=Т, найдем
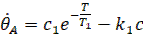
Подставляя (8), имеем в виду, что 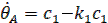 получим
получим
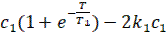 (9)
(9)
в котором содержатся две неизвестных 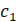 и Т.
и Т.
Длительность участка АВ=Т можно выразить из (5), т.к. известно, что в конце участка 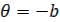 . Из (5) и (6) при этом находим
. Из (5) и (6) при этом находим
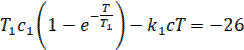
Подставляя значение 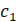 из (9), получим уравнение для определения полупериода автоколебаний:
из (9), получим уравнение для определения полупериода автоколебаний:
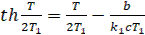 (10)
(10)
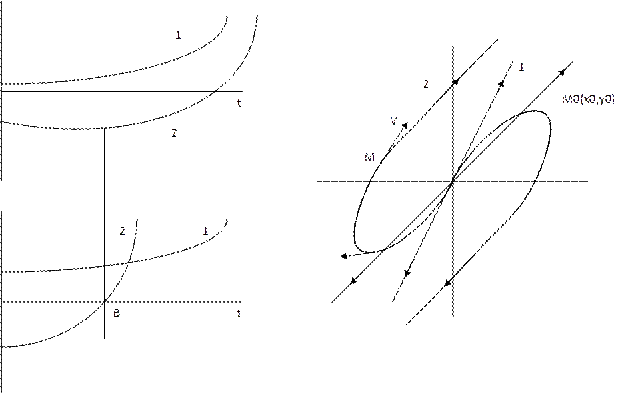
Если найдено вещественное положительное значение для Т, то это свидетельствует о наличии периодического решения в данной системе. Чтобы доказать, что это соответствует автоколебаниям, нужно исследовать на устойчивость, т.е. показать, что в переходном процессе система ведет себя как на рис (a). Амплитуда найденных автоколебаний определяется как 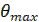 на участке АВ (рис. а) путем исследования функции (7) на максимум обычным путем.
на участке АВ (рис. а) путем исследования функции (7) на максимум обычным путем.
Фазовое пространство. Для наглядного представления о сложных нелинейных процессах регулирования прибегают к понятию фазового пространства, которое заключается в следующем. Дифференциальное уравнение замкнутой системы регулирования n-го порядка можно преобразовать к системе «n» дифференциальных уравнений первого порядка в виде
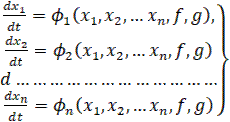 (11)
(11)
с начальными условиями
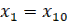 ,
, 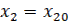 , …
, … 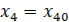 при t=0
при t=0
Где 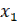 ,
, 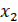 ,…,
,…, 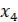 – переменные, являющиеся искомыми функциями времени, причем
– переменные, являющиеся искомыми функциями времени, причем 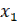 может обозначать результируемую величину, а
может обозначать результируемую величину, а 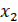 ,…,
,…, 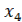 – вспомогательные переменные f, g – возмущающие и задающие воздействия.
– вспомогательные переменные f, g – возмущающие и задающие воздействия.
Пусть, например, в уравнениях (11) будет n=B. Переменные 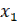 ,
,  ,
, 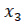 могут иметь любой физический смысл. Условно их можно представить мысленно как прямоугольные координаты некоторой точки М
могут иметь любой физический смысл. Условно их можно представить мысленно как прямоугольные координаты некоторой точки М

В реальном процессе регулирования в каждый момент времени величины 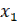 ,
,  ,
, 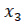 имеют вполне определенные значения. Это соответствует вполне определенному положению точки М в пространстве (рис.а). С течением времени в реальном процессе величины
имеют вполне определенные значения. Это соответствует вполне определенному положению точки М в пространстве (рис.а). С течением времени в реальном процессе величины 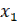 ,
,  ,
, 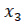 определенным образом изменяются. Это соответствует определенному перемещению точки М в пространстве по определенной траектории. Следовательно траектория движения точки М может служить наглядной геометрической иллюстрацией динамического поведения системы в процессе регулирования.
определенным образом изменяются. Это соответствует определенному перемещению точки М в пространстве по определенной траектории. Следовательно траектория движения точки М может служить наглядной геометрической иллюстрацией динамического поведения системы в процессе регулирования.
Точка М называется изображающей точкой, ее траектория называется фазовой траекторией, а пространство ( 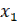 ,
,  ,
, 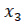 ) называется фазовым пространством.
) называется фазовым пространством.
Фазовое пространство и фазовые траектории представляют собой геометрические образы динамических процессов, протекающих в системе. В этом геометрическом представлении исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количественно положение изображающей точки в любой момент времени, нужно найти решение заданных дифференциальных уравнений (11) во времени.
Если уравнения (11) в отклонениях от установившегося состояния, то последнее характеризуется значениями  . Следовательно, изображением установившегося состояния системы является начало координат фазового пространства.
. Следовательно, изображением установившегося состояния системы является начало координат фазового пространства.
Отсюда следует, что фазовые траектории линейной системы будут приближаться к началу координат при неограниченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Для нелинейной системы вследствие ряда особенностей процессов фазовые траектории могут принимать самые разнообразные очертания. Если имеется асимптотическая устойчивость ля определенного круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области η, окружающей начало координат фазового пространства (рис.б), будут асимптотически приближаться к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри определенной области η вокруг начала координат фазового пространства, могут иметь любые очертания, но не будут выходить за пределы некоторой определенной области Ԑ, окружающей начало координат.
Формулировка понятия устойчивости по Ляпунову.
Невозможное движение (установившийся процесс называется устойчивым, если при заданной сколь угодно малой области Ԑ (рис.б) можно найти такую область η, что при начальных условиях, возмущенное движение (переходный процесс) будут таким, что изображающая точка не выйдет из области Ԑ при любом сколь угодно большом значении времени t.
В аналитической постановке определения устойчивости запись условия выглядит следующим образом: невозмущенное движение (уст. Процесс) будет устойчивым, если при заданных положительных сколь угодно малых числах  можно найти такие положительные числа
можно найти такие положительные числа 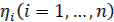 , что при начальных условиях
, что при начальных условиях
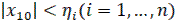 (12)
(12)
решение дифференциального уравнения возмущенного движения (переходного процесса) удовлетворяет неравенствам
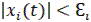
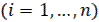
при любом сколь угодно большом t, начиная с некоторого 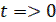 .
.
Фазовые траектории для обыкновенных систем.
Пусть переходный процесс в некоторой системе описывается уравнениями второго порядка
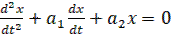 (13)
(13)
Введем обозначение для скорости изменения отклонения регулируемой величины 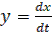 . Тогда уравнение системы (13) преобразуется к виду
. Тогда уравнение системы (13) преобразуется к виду
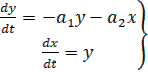 (14)
(14)
Исключим из уравнений (14) время (t), разделив первое из них на второе при x и y≠0
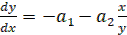 (15)
(15)
Решение 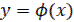 этого дифференциального уравнения с одной произвольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (x,y), каждая из которых соответствует одному определенному значению произвольной постоянной.
этого дифференциального уравнения с одной произвольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (x,y), каждая из которых соответствует одному определенному значению произвольной постоянной.
Уравнению (13) соответствуют корни характеристического уравнения 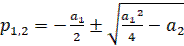
при этом возможно шесть случаев:
1) Корни часто мнимые при 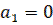 ,
,  (граница устойчивости линейной системы);
(граница устойчивости линейной системы);
2) Корни комплексные и имеют отрицательные вещественные части при 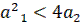 ,
, 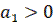 ,
, 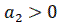 (устойчивая линейная система);
(устойчивая линейная система);
3) Корни комплексные и имеют положительные вещественные части при 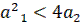 ,
, 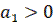 ,
,  (неустойчивая линейная система);
(неустойчивая линейная система);
4) Корни вещественные отрицательные при 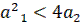 ,
, 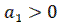 ,
,  (устойчивая линейная система);
(устойчивая линейная система);
5) Корни вещественные положительные при 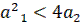 ,
, 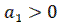 ,
,  (неустойчивая линейная система);
(неустойчивая линейная система);
6) Корни вещественные и имеют разные знаки при  (неустойчивая линейная система); в частности один из корней устойчивости линейной системы.
(неустойчивая линейная система); в частности один из корней устойчивости линейной системы.
Случай 1
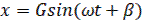 ;
; 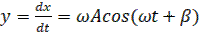
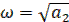 (16)
(16)
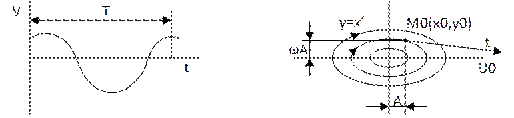
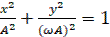 – уравнение эллипса.
– уравнение эллипса.
Случай 2
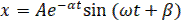 ,
, 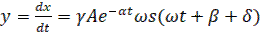
Где
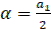 ,
, 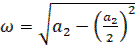 ;
; 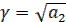 ;
; 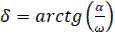 .
.
Произвольные постоянные А и 𝛃 определяются из начальных условий: 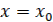 ,
, 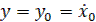 t=0.
t=0. 
Случай 3

Случай 4
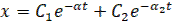
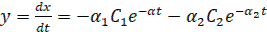 (17)
(17)
где 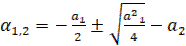

Случай 5
Случай 6
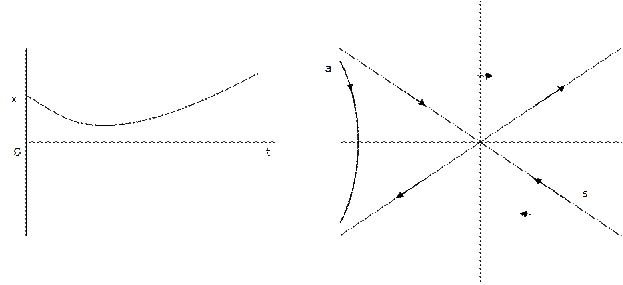
Уравнения систем с нелинейностью релейного типа
Уравнения систем с нелинейностью релейного типа
Система автоматического регулирования напряжения
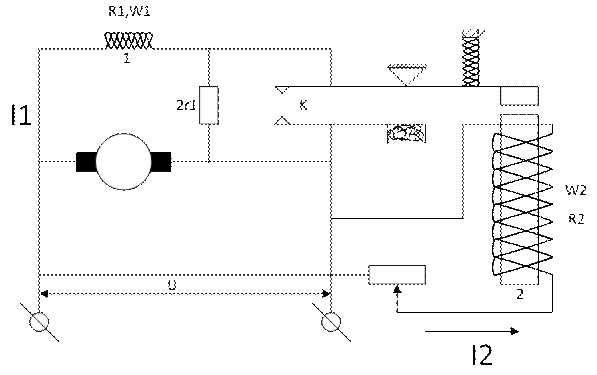
Когда контакты К под действием пружины П замкнуты, сопротивление 2r, выключено из цепи возбуждения генератора 1.
Система рассчитана так, что при этом напряжение U на клеммах генератора возрастает (при любой реально возможной нагрузке в сети, на которую работает данный генератор). В результате увеличивается ток 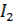 в катушке 2 электромагнитного реле и якорь реле притягивается, размыкая тем самым контакты К. При разомкнутых же контактах К в цепь возбуждения включено сопротивление 2r. Это вызывает снижение напряжения U, и значит уменьшение тока
в катушке 2 электромагнитного реле и якорь реле притягивается, размыкая тем самым контакты К. При разомкнутых же контактах К в цепь возбуждения включено сопротивление 2r. Это вызывает снижение напряжения U, и значит уменьшение тока 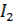 и отпускание реле, в результате чего контакты К снова замыкаются, выключая тем самым сопротивление 2r, из цепи возбуждения. Настройка системы на желаемое номинальное значение регулируемой величины U и производится установкой системы
и отпускание реле, в результате чего контакты К снова замыкаются, выключая тем самым сопротивление 2r, из цепи возбуждения. Настройка системы на желаемое номинальное значение регулируемой величины U и производится установкой системы 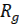 .
.
Уравнение регулируемого объекта (генератора) представим в линейном виде:
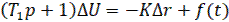 (18)
(18)
где Δr – изменение сопротивления цепи возбуждения (регулирующее воздействие). Постоянная времени 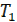 и коэффициент
и коэффициент 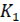 определяются параметрами якоря и цепи возбуждения.
определяются параметрами якоря и цепи возбуждения.
Уравнение чувствительного элемента (электромагнит 2) запишем в виде
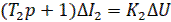 (19)
(19)
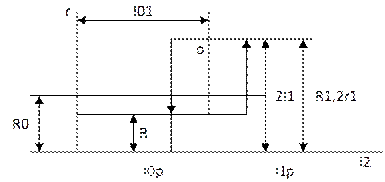
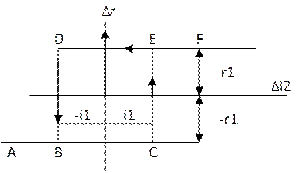
Регулирующий орган (контакты К, скачком включающие и выключающие сопротивление 2r1) являются нелинейным звеном релейного типа. Выходная величина его – сопротивление r цепи возбуждения – меняется скачкообразно при срабатывании и отпускает реле, т.е. в зависимости от величины тока 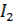 в цепи катушки 2 электромагнитного реле (рис. а) и б)). Здесь Iср и Iопт – токи полного срабатывания и отпускания реле.
в цепи катушки 2 электромагнитного реле (рис. а) и б)). Здесь Iср и Iопт – токи полного срабатывания и отпускания реле.
Для составления уравнений такого нелинейного звена удобно ввести отклонения 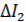 и
и  от некоторых постоянных значений
от некоторых постоянных значений 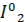 и
и 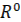 .
.
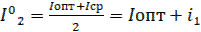 ,
,
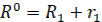 .
.
Уравнение нелинейного звена (рис. б) будет
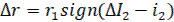 при
при 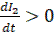 (20)
(20)
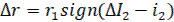 при
при 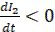 (21)
(21)
Формулы (20) и (21) отвечает соответственно движению вправо по линии ABCEF и влево по линии FEDBA, причем в точках C и D происходит переключение реле (перескоки b(1)E и B соответственно).
Уравнения линейной части системы (18) и (19) при f(t)=0, объединим в одно:
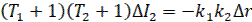 (22)
(22)
Постоянные значения, от которых производится здесь отсчет отклонений переменных, определяется из алгебраических уравнений условно номинального установившегося режима
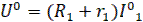 ;
;
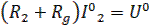 ;
;
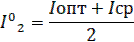
с использованием реальных характеристик генератора.
Частный метод В.Н. Попова.
Решение задачи исследования устойчивости системы с нелинейностью любого очертания на основе частотного метода предложено румынским ученым В.Н. Поновым.
Если в САУ имеется лишь одна однозначная нелинейность
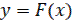 , (1)
, (1)
то, объединив все остальные (линейные) уравнения системы, можно всегда получить общее уравнение линейной части системы (см. рис. а) в виде

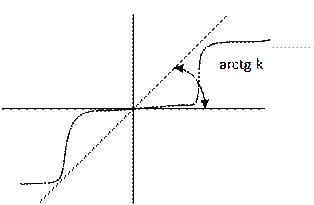
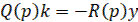 (2)
(2)
где
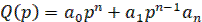
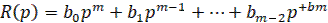
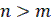
Пусть нелинейность y=F(x) имеет любое очертание, но выходящее за пределы заданного угла arctg k (рис. б), т.е. при любом x
 (3)
(3)
Пусть многочлен, или, что то же, характерное уравнение линейной части Q(p)=0 имеет все корни с отрицательными вещественными частями или же кроме них имеется еще не более двух нулевых корней. Другими словами допускается, чтобы 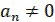 или
или 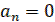 и
и 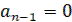 в выражении Q(p), т.е. не более двух нулевых полюсов в передаточной функции линейной части системы
в выражении Q(p), т.е. не более двух нулевых полюсов в передаточной функции линейной части системы
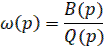
Теория В.Н. Понова: для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором при всех 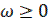
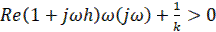 (4)
(4)
где 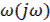 – амплитудно-фазовая частотная характеристика линейной части системы. При наличии одного нулевого полюса требуется еще, чтобы
– амплитудно-фазовая частотная характеристика линейной части системы. При наличии одного нулевого полюса требуется еще, чтобы
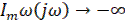
при 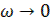 ,
,
а при двух нулевых полюсах
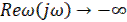
при 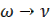 ,
,
а 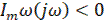 при малых 𝛚.
при малых 𝛚.
Теорема справедлива также и при наличии в знаменателе Q(p) передаточной функции линейной части не более двух чисто мнимых корней.
В другой формулировке теоремы дающую удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики 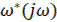 , которая определяется следующим образом:
, которая определяется следующим образом:
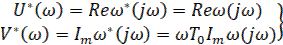 (5)
(5)
где 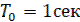 – нормирующий множитель.
– нормирующий множитель.
Тогда в новом определении В.Н. Понова: для установления устойчивости линейной системы достаточно подобрать такую прямую на плоскости 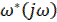 , проходящую через точку (
, проходящую через точку ( 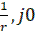 ), чтобы вся кривая
), чтобы вся кривая 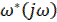 лежала справа от этой прямой. На рис. (а), (б) показаны случаи устойчивости системы.
лежала справа от этой прямой. На рис. (а), (б) показаны случаи устойчивости системы.
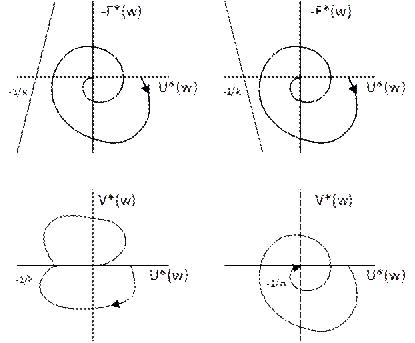
ЛИТЕРАТУРА
1.Солодовников В.В. Основы теории и элементы систем автоматического регулирования. М. Машиностроение ,1985
2.Под редакцией Солодовникова В.В. Техническая кибернетика. Теория автоматического регулирования. Книга 1,2. М. Машиностроение, 1967
3.Воронов А.А. Основы теории автоматического регулирования. М., В.Ш. , 1977
4.Бесекерский В.А. , Попов Е.П. Теория систем автоматического регулирования. М.,Наука,1975
5.Ройтенберг Я.Н. Автоматическое управление. М., Наука, 1978
6. Востриков А.С., Французова Г.А. Теория автоматического регулирования. - М: Высшая школа, 2004.
7.Анкимюк В.Л., Опейко О.Ф., Михеев Н.Н.. Теория автоматического управления.. – М: Дизайн ПРО,2002.
Литература.
Основная литература.
1. Бесекерский В.А., Попопв Е.П. Теория систем автоматического управления. – СПб.:Профессия,2003.
2. Подчукаев В.А. Теория автоматического управления. – М.:Физматлит,2005.
3. Ерофеев А.А. Теория автоматического управления – СПб.:Политехника,2005.
4. Гальперин М.В. Автоматическое управление-М.: ИД «Форум»-
5. Ким Д.П. Теория автоматического управления, т.1,т.2.-М.:Физматлит,2004. ИНФРАМ, 2007.
6. Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев Б.В. Теория автоматического управления – М.: Высшая школа, 2005.
7. Востриков А.С., Французова Г.А. Теория автоматического регулирования – М.:Высшая школа,2004.
8.
9. Анкимюк В.Л., Опейко О.Ф., Михеев Н.М. Теория автоматического управления. – М.:Дизайн ПРО,2002.
Дополнительная литература.
1. Савин М.Н., Елсупов В.С, Пятина Е.Н. Теория автоматического управления – Ростов-на-Дону: Феникс,2007
2 Дорф.Р., Бишоп Р. Современные системы управления. – М.: Лаборатория базовых знаний,2004.
3. Под редакцией Пупкова К.А. Методы классической и современной теории автоматического управления. – М.:, МГТУ,2000.
4. Филипс Ч.,Харбор Р. Системы управления с обратной связью. М.: Лаборатория базовых знаний,2001.
Дата добавления: 2019-09-30; просмотров: 658;











