Конечно-разностные методы

Применение конечно-разностных методов к краевым задачам в основном сводится к довольно тривиальной процедуре. Любая производная в дифференциальном уравнении заменяется соответствующей конечно-разностной аппроксимацией.

Рассмотрим, например, линейное дифференциальное уравнение вида

y'' + p(x)y' +q(x)y = f(x), a < x < b (6.20)

с граничными условиями

x=a: a₁y(a) +b₁y'(a)=g₁; (6.21)

x=b: a₂y(b) +b₂y'(b)=g₂. (6.22)

Введем на отрезке [a, b] разностную сетку a = x₀, x₁, x₂,…, x_N = b с шагом .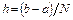

В каждой внутренней точке заменим производные центральными разностями (аппроксимация порядка O(h²)). Получаем систему разностных уравнений:

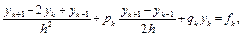(6.23)

k=1, 2, … ,N–1.

Построим разностную аппроксимацию краевых условий со вторым порядком точности. Для этого разложим y₁ в ряд Тейлора в окрестности точки x₀:

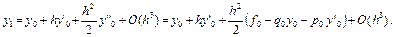
Отсюда .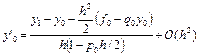

Аналогично для точки x_N-1.

.

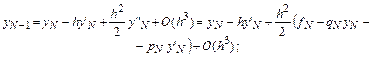
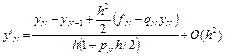Разностные уравнения (6.2) вместе с граничными соотношениями составляют систему из N+1 линейных алгебраических уравнений с N+1 переменной y₀, y₁, …, y_N.

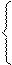y₀ + l₁y₁ = m₁;

a_ky_k–1 + c_ky_k + b_ky_k+1 = d_k; k=1…N–1;(6.24)

l₂y_N–1 + y_N = m₂;

где a_k = 1 – 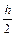p_k; c_k = h²q_k –2; b_k = 1 + 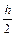p_k; d_k = h²f_k.

Или в развернутом виде:

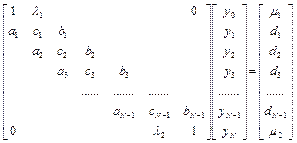
Таким образом, краевая задача сводится к решению системы уравнений c трехдиагональной матрицей:

Ay = d.

Мы уже знаем, что для решения СЛАУ с трехдиагональной матрицей используется метод прогонки. Известно, что для устойчивости прогонки необходимо диагональное доминирование матрицы коэффициентов, т.е.

|c_k| ³ |a_k| + |b_k|; 1 ³ |l₁|; 1 ³ |l₂|

или в нашем случае

| h²q_k – 2| ³ |1–hp_k /2| + |1+hp_k /2|.

Из этого соотношения можно получить ограничение на шаг для конкретных значений q_k, p_k.

Сходимость же решения (и область сходимости) необходимо исследовать особо. Или – другой путь. Провести расчет для разных значений шага (не менее трех) и убедиться в том, что полученные значения функции в одних и тех же узлах близки между собой и их разность уменьшается, что говорит о стремлении решения к некоторому пределу при h®0.

Если же краевая задача нелинейная (нелинейно уравнение и/или граничные условия), то в результате применения конечно-разностного метода получается система нелинейных уравнений

A(x,y)y = d(x,y) или F(y) = 0.

Для решения систем нелинейных уравнений используются в основном итерационные способы, например метод Ньютона:

y^(m+1) = y^(m) – F(y^(m))/F′(y^(m)),

где F′(y^(m)) – матрица Якоби.

Метод стрельбы

Суть метода стрельбы заключается в сведении решения краевой задачи к решению задач Коши.

Рассмотрим его применение на примере той же задачи (6.20).

Обозначим z(x)=y¢.Получаем краевую задачу для системы из двух дифференциальных уравнений первого порядка:

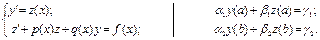(6.25)

Зададим произвольно еще одно условие, например, на левой границе: y(a)=x.

Тогда .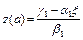

Следовательно, мы можем начать решение задачи Коши для системы из двух уравнений. Решаем каким-либо из известных нам методов, например, методом Рунге-Кутта и находим решение в точке x=b. Естественно, это решение получилось у нас зависящим от x: y_N(x), z_N(x). Более того, это решение должно удовлетворять правому граничному условию (при x=b), т.е. необходимо, чтобы

a₂y_N(x) + b₂z_N(x) = g₂ или F(x) = 0. (6.26)

Таким образом, наша задача свелась к поэтапному улучшению первоначальной оценки граничного условия y(a) = x до тех пор, пока условие (6.26) не выполнится, т.е. к «пристрелке».

В общем случае уравнение (6.26) нелинейно и решается относительно x любым из известных способов решения нелинейных уравнений (итераций, Ньютона, половинного деления и т.п.). Функция F(x) в явном виде неизвестна, однако ее значение можно вычислить для любого заданного x путем решения задачи Коши.

Таким образом, процесс реализации метода стрельбы можно разбить на три этапа:

1) подбор хорошего начального приближения для x;

2) нахождение эффективного метода вычисления F(x);

3) выбор соответствующего итерационного метода для решения уравнения F(x)=0.

Если система уравнений (6.25) содержит больше двух уравнений, то недостающих условий на каком-либо конце отрезка интегрирования будет больше, чем одно.

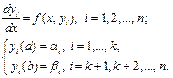(6.27)

В этом случае поступают аналогичным образом.

Во-первых, выбирают границу с большим числом заданных граничных условий, пусть это будет x=a, а недостающие задают произвольным образом: y_i(a)=x_i, i=k+1,…,n.

Во-вторых, решают задачу Коши и находят

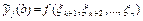, j=1,…, n.

Теперь на правой границе необходимо решать систему нелинейных (в общем случае) уравнений

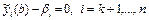или F(x) = 0 (6.28)

для нахождения необходимых значений x_i. Эта задача также решается одним из известных методов (метод Ньютона, методы спуска).

Решение задачи Коши, при котором выполнится (6.28), и будет решением краевой задачи.

Отметим еще следующее. «Пристрелку» можно вести и с двух концов одновременно, задавая произвольным образом недостающие граничные условия на обоих концах отрезка и решая задачу Коши одновременно с двух сторон (из точки х=а и x=b). Некоторая точка встречи решений называется точкой сшивания (x=x_m). В этой точке должны выполняться условия сшивания:

F(x) º y_i(a, x_m, x) – y_i(b, x_m, x) = 0.

Правильный выбор положения точки x_m позволяет преодолеть некоторые трудности, которые возникают в процессе практического интегрирования уравнений.

Если система дифференциальных уравнений неустойчива в одном направлении, то можно проводить интегрирование в противоположном направлении, выбрав в качестве точки сшивания соответствующий конец отрезка. Если система неустойчива в обоих направлениях, то влияние неустойчивости можно минимизировать, смещая точку сшивания к середине отрезка интегрирования.

Отметим также, что метод стрельбы малопригоден, если имеется сильная зависимость функции F(x) от начального значения x. В этом случае следует очень точно определять это начальное значение, что не всегда возможно.