Использование z – преобразования.

Для решетчатых функций может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

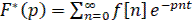(16)

Для смещенных решетчатых функций может быть записано аналогичное выражение:

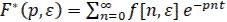(17)

Формулы (16) и (17) можно представить в символической записи

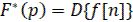(18)

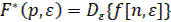(19)

В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина 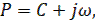где с – абсцисса абсолютной сходимости. Если 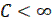, то ряд, определяемый формулами (16) и (17), сходится к решетчатой функции соответствует некоторое изображение.

Для исследования ИСАУ большое распространение получило так называемое z – преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него.

Под z – преобразованием понимается изображение несмещенной или смещенной решетчатой функций, определяемое формулами:

,

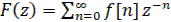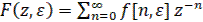(20)

В формулах введено новое обозначение 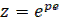. Из них следует что z – преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только аргументом изображения.

Формулы преобразования (20) записываются в символической форме:

,

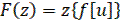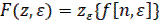(21)

Формулы преобразования (21) могут быть записаны и для непрерывной производящей функции в виде

,

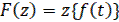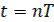
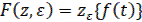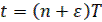, (22)

где n = 0, 1, 2,…

Ряды (20) сходятся и изображение решетчатой функции существует, если выполняется условие, сформулированное выше для дискретного преобразования Лапласа: 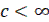, где с – абсцисса абсолютной сходимости.

Единичная импульсная решетчатая функция

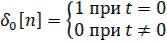(23)

Изображение решетчатых функций

Производящая непрерывная функция	Несмещенная решетчатая функция	z-преобразование
Оригинал	Изображение Лапласа	простое	смещенные
	-
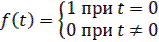
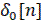
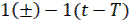
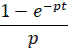
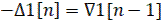
1(t)		1[n]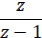
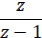
t		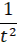nT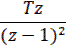

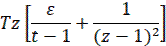
Операцию нахождения z-преобразования от решетчатой функции (21) или от непрерывной производящей функции (22) можно распространить на изображение Лапласа непрерывной производящей функции

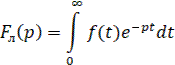
Пусть решетчатая функция f[nT] получается из непрерывной функции f[t] квантованием в моменты времени t=nT. Введем вспомогательную импульсную функцию, образованную умножением исходной непрерывной функции на последовательность δ-функции

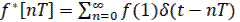(24)

Найдем преобразование Лапласа введённой функции

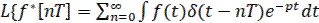(25)

Т.к. интеграл от δ-функции равен единице, то имеем

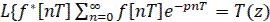(26)

где .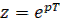

Таким образом, преобразование Лапласа для импульсной функции оказывается равным z-преобразованию исходной непрерывной производящей функции.

Обозначив последовательность δ-функции вида 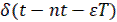, где n=0,1,2, через 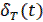импульсную функцию при ε≠0, можно представить следующим образом:

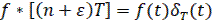(27)

Применим к левой и правой частям последнего выражения преобразования Лапласа. В соответствии с приведённым доказательством в левой части будет получено z-преобразование исходной непрерывной функции времени

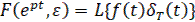(28)

Используя теорему свертки в комплексной области

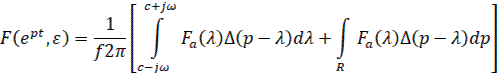
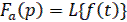(30)

Кроме того

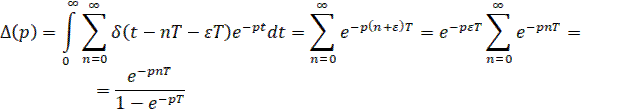
Окончательное выражение для искомого z-преобразования будет при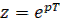

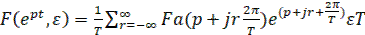(31)

При любом ε˃0

При ε=0

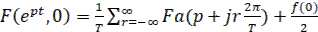(32)