НЕЯВНЫЕ РАЗНОСТНЫЕ ФОРМУЛЫ
До сих пор мы записывали явные разностные схемы, т.е. необходимое значение функции определялось явным образом по известным точкам.
Для некоторого класса задач широко используются также неявные схемы. Рассмотрим один из способов их получения.
Аппроксимируем подынтегральную функцию интерполяционным полиномом Ньютона Nn+1(x), т.е. начнем с точки xn+1, а не с точки xn, как это мы делали в п.6.3.
Тогда для x = xn+th имеем
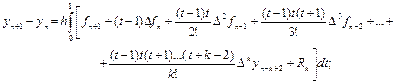
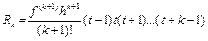 .
.
Проведя интегрирование, получаем неявную (интерполяционную) формулу Адамса (в разностном виде):
yn+1 = yn + h(fn+1 – 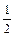 Dfn –
Dfn – 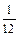 D2fn–1 –
D2fn–1 – 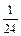 D3fn–2 –
D3fn–2 –
–  D4fn–3 –
D4fn–3 – 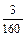 D5fn–4 – …). (6.15)
D5fn–4 – …). (6.15)
Получим конкретные интерполяционные формулы Адамса в ординатном виде:
1) yn+1 = yn + h fn+1 (неявная формула Эйлера). (6.16)
Формула первого порядка. Локальная погрешность 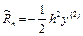 ;
;
2) yn+1 = yn + h fn+1 – 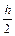 Dfn =
Dfn =
= yn + h fn+1 – 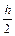 (fn+1 – fn) = yn +
(fn+1 – fn) = yn + 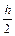 (fn+1 + fn) (6.17)
(fn+1 + fn) (6.17)
Формула второго порядка. Локальная погрешность 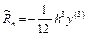 ;
;
3) yn+1 = yn + h(fn+1 – 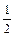 Dfn –
Dfn – 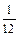 D2fn–1)
D2fn–1)
= yn + 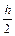 (fn+1 + fn) –
(fn+1 + fn) – 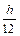 ( fn+1 – 2fn + fn–1) =
( fn+1 – 2fn + fn–1) =
= yn + 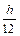 (5fn+1 + 8fn – fn–1). (6.18)
(5fn+1 + 8fn – fn–1). (6.18)
Формула третьего порядка. Локальная погрешность 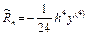 ;
;
4) yn+1 = yn + h(fn+1 – 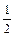 Dfn –
Dfn – 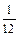 D2fn–1 –
D2fn–1 – 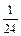 D3fn–2) =
D3fn–2) =
= yn + 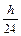 (9fn+1 + 19fn – 5fn–1 + fn–2). (6.19)
(9fn+1 + 19fn – 5fn–1 + fn–2). (6.19)
Формула четвертого порядка. Локальная погрешность 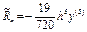 .
.
В принципе, целый класс неявных разностных формул можно получить интегрированием интерполяционного многочлена Ньютона по отрезку [xn–j, xn+1], j ³1 (при j = 0 – неявные формулы Адамса). Это приводит к неявным разностным формулам Милна.
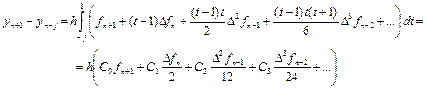
| C0 | C1 | C2 | C3 | |
| j = 1 | –4 | |||
| j = 2 | –9 | –9 | ||
| j = 3 | –16 | –64 |
Например, в ординатном виде для j=1 получаем неявную формула Милна четвертого порядка (только по двум точкам!):
yn+1 = yn–1 + 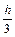 (fn+1 + 4fn + fn–1).
(fn+1 + 4fn + fn–1).
Локальная погрешность 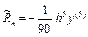
Знакомая формула, знакомая погрешность (см. формулу Симпсона). Т.е. здесь просто интеграл заменяется известной квадратурной формулой.
В чем недостаток неявных разностных формул по сравнению с явными?
Для нахождения искомого значения функции y необходимо в общем случае организовывать итерационный процесс, т.е. использовать те или иные формулы приближенного решения трансцендентных уравнений.
В чем преимущество неявных разностных формул?
1. Используют меньше точек, чем соответствующие явные схемы.
2. Их точность выше, чем у соответствующих явных схем (сравните локальные погрешности формул (6.16) и (6.11), (6.17) и (6.12), (6.18) и (6.13)).
3. Шире диапазон устойчивости по сравнению с явными схемами.
С последним достоинством неявных разностных схем следует разобраться более подробно.
Для каждой конкретной дифференциальной задачи и конкретной разностной схемы существует диапазон устойчивости схемы, который определяется ограничениями, накладываемыми на шаг разностной схемы. Речь идет о том, каким максимально большим может быть шаг, чтобы решение было устойчивым.
Проиллюстрируем это на примере.
Пример. Рассмотрим линейное уравнение вида:
y′ = ly, y(0) =y0, l < 0 – некоторая константа.
Точное решение этой задачи y(x) = elxy0. При возрастании x это решение убывает, сохраняя знак.
1. Для явного метода Эйлера имеем
yn+1 = yn + hlyn = (1 + hl)yn.
Потребуем, чтобы решение разностной схемы обладало таким же свойством, как и точное решение. Очевидно, что условием такого поведения решения является выполнение неравенства
0 < 1+lh < 1 Þ |l|h <1.
Таким образом, есть ограничение на шаг:
h <1/|l|.
2. Для явного метода Рунге-Кутта второго порядка:
yn+1 = yn + 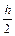 (lyn + l (yn + hl yn)) = yn(1 + hl +
(lyn + l (yn + hl yn)) = yn(1 + hl + 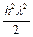 ).
).
Чтобы решение этой разностной задачи монотонно убывало, необходимо выполнение условия
0 < 1 + hl + 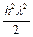 < 1 или –2 < lh(lh + 2) < 0;
< 1 или –2 < lh(lh + 2) < 0;
–2 < lh < 0;|l|h <2.
Ограничение на шаг: h <2/|l|.
3. Для явного метода Адамса второго порядка:
yn+1 = yn + 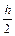 (3lyn – lyn–1) = yn(1 +
(3lyn – lyn–1) = yn(1 + 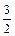 hl) –
hl) – 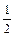 hl yn–1;
hl yn–1;
yn+1 – (1 + 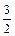 hl)yn +
hl)yn + 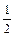 hl yn–1 = 0.
hl yn–1 = 0.
При анализе устойчивости этой схемы (она уже двухшаговая, в отличие от предыдущих одношаговых) получить критерий устойчивости таким же способом не удается. Поэтому используеем другой (более общий) способ анализа.
Запишем для удобства это уравнение в виде
yn+2 – (1 + 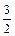 hl)yn+1 +
hl)yn+1 + 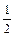 hl yn = 0.
hl yn = 0.
Общее решение этого уравнения: yn = C1yn(1) + C2yn(2) (сумма двух линейно независимых решений). Это следует из теории дифференциальных уравнений. Будем искать линейно независимые решения в виде: yn = qn,где q ¹ 0 – некоторое число.
После подстановки получаем квадратное уравнение
q2 – (1 + 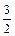 hl)q +
hl)q + 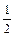 hl = 0.
hl = 0.
Его дискриминант
D = (1 + 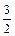 hl)2 – 2hl = 1 + hl +
hl)2 – 2hl = 1 + hl + 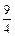 (hl)2 > 0при любых hl.
(hl)2 > 0при любых hl.
Следовательно, q1 и q2 действительны и различны.
Устойчивость означает |q1|<1, |q2|<1.
Воспользуемся следующим свойством квадратного уравнения q2+bq+c=0: корни уравнения не превосходят по модулю единицу, если
|b| £1 + c, c £ 1Þ |1 + 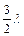 h| £1 +
h| £1 + 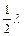 h;
h; 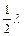 h £1;
h £1;
|2 + 3lh| £ 2 + lh; |lh| £1.
Ограничение на шаг: h <1/|l|.
4. Неявный метод Эйлера (или неявный метод Адамса первого порядка)
yn+1 = yn + hlyn+1; 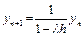 ;
;
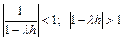 , что для l<0 выполняется всегда.
, что для l<0 выполняется всегда.
5. Неявный метод Адамса второго порядка.
yn+1 = yn + 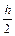 (fn+1 + fn) = yn +
(fn+1 + fn) = yn + 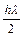 (yn+1 + yn)
(yn+1 + yn)
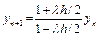
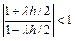 ,
,
что для всех l<0 выполняется всегда.
Конечно, не все неявные схемы безусловно устойчивы, например, неявная схема Адамса третьего порядка
yn+1 = yn + 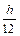 (5fn+1 + 8fn – fn–1)
(5fn+1 + 8fn – fn–1)
устойчива при |lh|<6. Сравните, явная схема Адамса третьего порядка имеет область устойчивости |lh|<0.545.
Таким образом, мы видим, что при использовании явных схем существуют довольно жесткие ограничения на шаг. Например, для модельной задачи они имеют вид h £ C/|l|.
При больших |l| это условие ограничивает выбор шага. Отсюда и возник термин жесткие уравнения. Подчеркнем, что жесткость – это свойство уравнения, а не численной схемы. Следовательно, для обеспечения устойчивости явной схемы необходимо выбирать очень маленький шаг интегрирования, что приводит к большому числу шагов на больших промежутках интегрирования и, как следствие, чрезмерному возрастанию времени решения задач на ЭВМ и увеличению вычислительной погрешности.
ЖЕСТКИЕ ЗАДАЧИ
Жесткие уравнения – такие уравнения, которые моделируют процессы, обладающие свойством жесткости. Подобные процессы описываются суперпозицией функций двух видов: с большими по модулю производными и с малыми по модулю производными, причем функции с большими производными быстро изменяются. Такие задачи часто встречаются при исследовании динамических систем в химической кинетике, электротехнике, механике сплошных сред, в теории управления.
Для численного моделирования быстропротекающих процессов необходим малый шаг интегрирования. Однако на тех участках, где существенны функции с малыми производными, уменьшение шага ведет к увеличению погрешности (вычислительной) и увеличению времени решения задачи. Указанным дефектом страдают явные методы, для которых существуют ограничения на шаг.
Рассмотрим систему дифференциальных линейных уравнений вида:
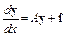 ,
,
где y и f – векторы, A = {ai,j} – постоянная матрица, у которой все собственные значения li имеют отрицательные вещественные части (i, j = 1, …, M). Таким свойством обладает, например, симметричная матрица. Общее решение записанной системы уравнений может быть представлено в виде суммы частных решений
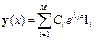 ,
,
где 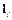 - собственный вектор, соответствующий собственному значению li.
- собственный вектор, соответствующий собственному значению li.
Эту систему называют жесткой, если отношение
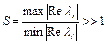 ,
,
где S – коэффициент жесткости.
На практике система считается жесткой, если S > 10, однако в задачах химической кинетики, в задачах управления, в расчетах электрических цепей коэффициент S достигает величин ~106 и более.
Посмотрим на поведение решения для жесткой системы из двух уравнений:
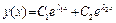 .
.
Пусть 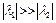 и l – вещественные.
и l – вещественные.
Для того чтобы смоделировать первую составляющую решения, необходим очень мелкий шаг (т.к. оно быстро затухает). Казалось бы, после прохождения первого промежутка, где скорость изменения решения определяется скоростью изменения первой составляющей, шаг интегрирования мог бы быть увеличен. Однако это сделать нельзя, т.к. в явных методах существует ограничение на шаг, обусловленное устойчивостью
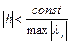
Получается так, что допустимый шаг определяется, фактически, той компонентой решения, которая быстрее убывает. Поэтому использование явных схем в таких ситуациях крайне нерационально.
Для решения жестких дифференциальных уравнений применяются неявные схемы. Хотя при этом приходится на каждом шаге решать в общем случае систему нелинейных уравнений, но за счет возможности значительно увеличить шаг h общий объем вычислений в случае использования неявных схем может быть существенно меньше, чем явных [11].
КРАЕВЫЕ ЗАДАЧИ
Краевые задачи появляются при решении уравнений высших порядков или систем уравнений. Напомним, что в них дополнительные условия задаются при двух значениях независимых переменных (например, на концах рассматриваемого отрезка).
Методы решения краевых задач можно в целом разделить на три основных класса:
1) конечно-разностные методы;
2) методы стрельбы (пристрелки);
3) приближенные методы (решение представляется в виде линейной комбинации некоторых базисных функций): метод коллокаций, метод Галеркина, метод Релея-Ритца.
Дата добавления: 2020-10-25; просмотров: 720;











