Выпуклость графика функции. Точки перегиба
Точка графика непрерывной функции 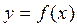 , отделяющая его части разной выпуклости, называется точкой перегиба.
, отделяющая его части разной выпуклости, называется точкой перегиба.
Теорема. Если функция 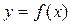 во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е.
во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. 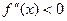 , то график функции в этом интервале выпуклый вверх.
, то график функции в этом интервале выпуклый вверх.
Если же 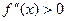 для любого
для любого 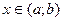 - график выпуклый вниз.
- график выпуклый вниз.
Теорема (достаточное условие существования точек перегиба).Если вторая производная 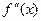 при переходе через точку
при переходе через точку 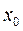 в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой 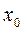 есть точка перегиба.
есть точка перегиба.
Общая схема исследования функции и построения
Графика функции
Исследование функции целесообразно вести в определенной последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции (промежутки, на которых 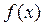 >0 или
>0 или 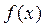 <0).
<0).
4. Выяснить, является ли функция четной, нечетной или общего вида.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности функции.
7. Найти экстремумы функции.
8. Найти интервалы выпуклости и точки перегиба графика функции.
Пример. Исследовать функцию 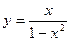 и построить ее график.
и построить ее график.
1. 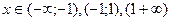
2. 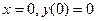
Точка (0;0)- точка пересечения графика с осями ОХ и ОУ.
3. Функция знакоположительна (у>0) в интервалах 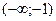 и
и 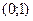 , знакоотрицательна – в
, знакоотрицательна – в 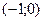 и
и 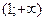
4. Функция 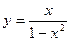 является нечетной т.к.
является нечетной т.к. 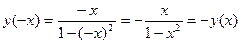 . Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при
. Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при 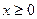 .
.
5. Прямые х = 1 и х = -1 являются ее вертикальными асимптотами.
Выясним наличие наклонной асимптоты.
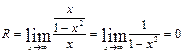
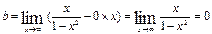
Следовательно, есть горизонтальная асимптота ее уравнение у=0. Наклонных асимптот нет.
Прямая у=0 является асимптотой и при 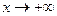 , и при
, и при 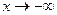 .
.
6. 
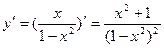 .
.
Так как у’>0 в области определения, то функции является возрастающей на каждом интервале области определения.
7. Т.к. 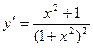 , то критическими точками является точки х1 = -1 и х2 = 1.
, то критическими точками является точки х1 = -1 и х2 = 1.
Данные точки не принадлежат области определения функции, значит, функция экстремумов не имеет.
8. Найдем 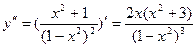
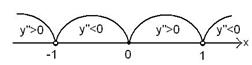
Точка (0;0) – точка перегиба графика функции.
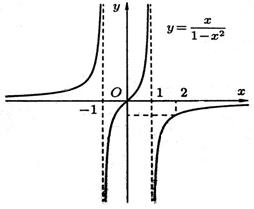 График выпуклый вверх на интервалах
График выпуклый вверх на интервалах 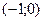 и
и 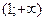 ; выпуклый вниз на интервалах
; выпуклый вниз на интервалах 
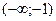 и
и 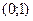
Дата добавления: 2021-01-26; просмотров: 667;











