Выпуклость и вогнутость графика функции. Точки перегиба.

О1. График функции 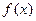называется выпуклым на интервале 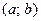, если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 81).

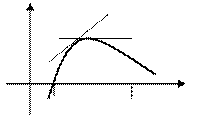
Рис. 81. Выпуклый график функции .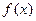

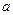
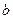
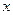
О2. График функции 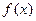называется вогнутым на интервале 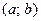, если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 82).

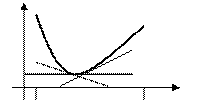
Рис. 82. Вогнутый график функции .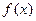

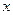
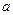
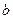
Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:

Т3. Если вторая производная функции 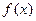на интервале 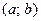существует и положительна, то на этом интервале график функции 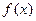будет вогнутым. Если вторая производная функции 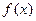на интервале 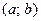существует и отрицательна, то на этом интервале график функции 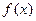будет выпуклым.

Пример 6. Определить интервалы вогнутости и выпуклости графика функции .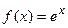

Найдем вторую производную от заданной функции 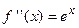. В силу того, что 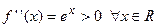, то график функции 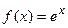будет вогнутым на всей числовой оси.

Пример 7. Определить интервалы вогнутости и выпуклости графика функции .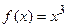

Найдем вторую производную от заданной функции 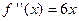. В силу того, что 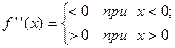, то график функции 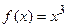будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.

О3. Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.

Выясним необходимые и достаточные условия существования точек перегиба.