Распределение Бозе и Ферми

Квантовая статистика невзаимодействующих тождесвенных частиц

Большое каноническое распределение

Было 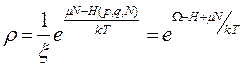(1)

(20 - стр 83)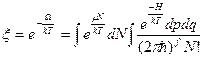

ξ- больш стат сумма

Ω=-PV - бошльшой термодин потенц

В квантовой статистике (анологично-тому что было для канон распр)

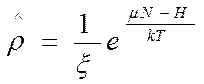и далее 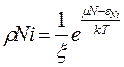(2)

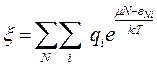(3)

(из усл нормировки), или, вводя Ω=-kTlnξ (4)

Ω(T,μ,N) и можно проверить что 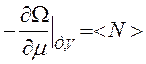согласуется с ТД

(2`)- верть того что сист содержит Т частиц и наход в iом кв сост, энерг сист Е_Ni

Распределение Бозе и Ферми

Рассмотрим идеальный газ тождественных микро частиц(Эл-ов атомов, ат ядядер..)Возможные сост кажд частицы характ дискретным набором квантовых чисел этот набор будем обозначать(характеризовать) вектором К и этому квантовому сост соотв енерг ε(к) (одной частицы) (анолог с излуч только не векторный потенц, а волн ф-я, тогда в сосуде с V=L³ одночастичное сот для одноатомного газа) опред набором 3х чисел {n_x n_y n_z} – kдля элементов в атомах: U(гл кв числа) lазимутальное m магнитное s спиновое

Пусть в к_ом сост. находится N_k частиц то N=∑_k N_k ; 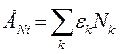(5)

Вся статистика теперь опр-ся числами заполнения N_k

(5) в (2) имеем

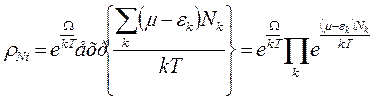(6)

т.е. произведение множителей последний из которых зависит от числа частиц N_k в состоянии кэнер

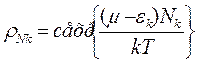(7)

и не зависит от др чисел заполнения

нормировка

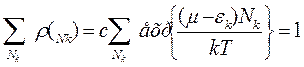(8)

здесь суммирование ведется по возможному числу частиц N_k в сост к

вычислим среднее число частиц в сост к

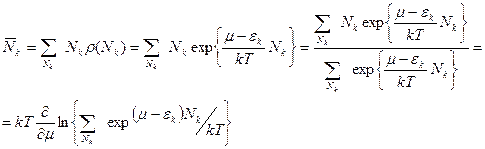(9)

Для бозонов N_k=0 1 2 3 может быть любым

Под логарифмом в (9) – геом прогрессия со знаменателем эта прогрессия сходится только при μ≤0!!! (ε_к>0) и 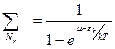(10`)

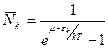(10) – распр-е Бозе- Эншт

Для фермионов спин принимает только 2 знач (0;1) (принцип запрета Паули) то

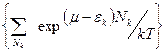
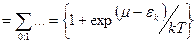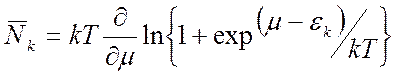
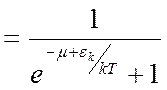(11`)

(11)

распределение Ферми Дирака – 1926.г

отличие между (10) и (11) – только знак перед 1

Заметим это(чисто формально),что при μ<0 |μ| >>1 (больше отрицательного μ) распределение Бозе и Ферми переходит в М-Б

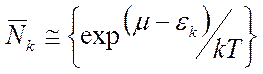(12) хим потенциал μ играет роль нормировочной константы. Из (12) видно, что ср число частиц в сост к N_k<<1 (μ<0) и частицы достаточно редко расположены в фазовом пр-ве

В квазиклас прибл. Кв сост в фаз.пр-ве опр-ся (как помним) ячейкой пр-ва с V=(2пћ)³=h³

Этой ячейке соотв (2S+1)-состояний отличающихся спином(спиновое вырожд)

Разберемся с конст в (12)в классике было:положимUk=0

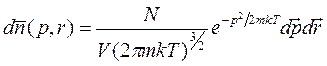(13)

среднее число частиц в ячейке dpdrпри это энерг ε_к=p²/2m найдем теперь

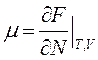свободную энергию вычислим

F=-N_kTlnV-3/2N_kTln(2пmkt) +3N_kTln(2пћ)+kTNlnN-kTN

Отсюда

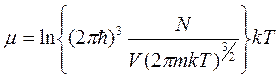(14)

сравним теперь (12) и (14) с (13)- видим:

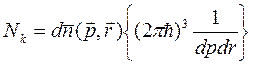(15)

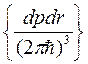число квантовых состоян ий в элементарной ячейке μ пр-ва – сходятся при учете вырождения N_k уменьш в (2S+1) раз N_k<<1

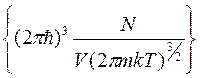<<1(16)

Вспомним:λ=2пћ/mv=h/mV длинна волны Де Броиля

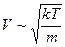тепловая скорость(средняя)

то

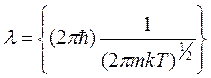-тепловая длинна волны Де броиля

V/N=1/n=l³

l- межчастичное расстояние, n-плотность. Тогда(16)

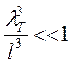(17) – условие классического приближения или не вырожденного газа - длинна волны Де Бройля мала по сравнению с раст м-ду частицами из (17) м-но ввести Твырожд

(18)

при Т>>Tвыр - класика

при T≤Tвыр –кв эффекты!!! Газ вырожд

Примеры

1)воздух при нормальной концентр N/V~10¹⁹1/sm³ m=μ/N* 30/6*10²³~5*10^-23

μ-молярная масса

(19)Твырожд=(6.6*10^-27*10 ¹³)2/(1.38*10^-16*5*10^-23)=6*10^-2K

2) электронный га в молек

N/V~5*10 ²²1/sm³ m 10-²⁷г

Tвыр=8*10⁴ K

1) плазма

1)утс N/V~10¹⁶ Tвыр=1.3*10^-3K м~4*10⁴

2)ионосфера N/V~10⁶ Tвыр стрем к 0

3)п\п N/V~10¹⁶ Tвыр=5К