Вырожденный бозе-газ.

Из условия нормировки (26), а также (14) следует, что активность А и химический потенциал μ растут при уменьшении T. Условие нормировки для бозонов:

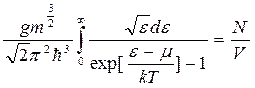(30)

При уменьшении T подынтегральная функция убывает (μ<0, ε-μ>0), и для компенсации этого убывания 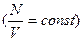надо увеличивать μ, то есть уменьшать его модуль .

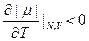Однако при некоторой температуре 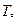химически потенциал достигает 0, причём:

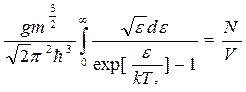(31)

Введём 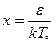, тогда

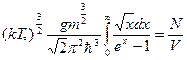(32) 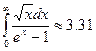- выражается через Г функцию

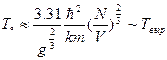(33)

Температура вырождения введена в (18). Выше 0 химический потенциал быть не может (иначе всё расходится), и при 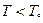μ=0 – условие нормировки уже выполняться не должно. В чём дело?

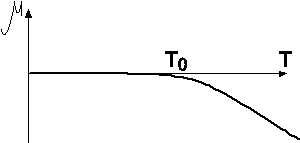
Условие нормировки может быть удовлетворено при N’<N!!! Дело в том, что при переходе от суммирования (в формуле (10’’)) к интегрированию (в (31)) – неточность членов суммы (10’’) 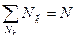с 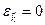(нулевого уровня). Они вклада не дают, так как умножаются на 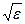, то есть выпадают из суммы. Математически:

При μ<0

ε→0: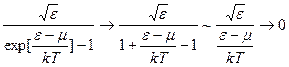

А уже потом μ→0

Таким образом, при понижении температуры частицы «конденсируются» на 0-й уровень энергии. Это – конденсация Бозе-Эйнштейна.

Тождественное условие нормировки теперь:

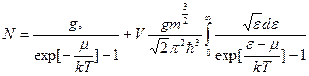
При 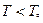μ<0 первое слагаемое мало (в 1/N раз)

при 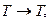μ→0 первое слагаемое растёт.

В действительности, при 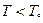частицы с энергией ε>0 распределены по формуле (*) с μ=0:

(**)

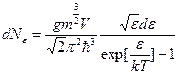А полное число частиц с ε>0 будет, следовательно (z=ε/kT):

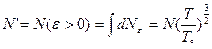(34)

Остальные частицы садятся на 0-й уровень:

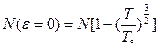
При 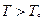- классические газы, при 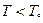- вырождение.

Конденсация Бозе-Эйнштейна происходит не в реальном , а в энергетическом пространстве. Совокупность частиц с ε=0 – конденсат. Энергия Бозе-газа в области конденсации (μ=0) равна:

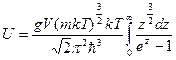(35)

Она определяется, конечно, частицами с ε>0.

Так как 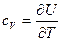, из (35) следует, что 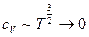при 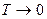(принцип Нернста выполнен)

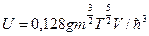
Давление (через уравнение состояния):

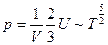- и не зависит от объёма!!! Только от температуры, так же как и при обычном фазовом равновесии газа с жидкостью (частицы с ε=0 давления не оказывают). При уменьшении объёма при 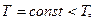число частиц с ε>0 уменьшается, а в конденсате растёт (фазовый переход первого рода!). Можно вычислять удельную теплоту перехода.

Реально: только жидкий гелий – существующая система бозе-частиц при низкой температуре. Остальные вещества кристаллизируются при T>>T_выр. У He при T≈219°К происходит переход в сверхтекучее состояние. Однако, для объяснения приходится учитывать неидеальность.

Фотонный газ.

Рассматривали равновесное излучение (чёрное излучение) – как равновесие волн со средой. Однако, наряду с волновыми свойствами излучение обладает свойствами корпускулярными (дуализм). Интерференция – проявляются волновые свойства, фотоэффект – корпускулярная природа.

С корпускулярной точки зрения свет – поток квантов – фотонов с энергией 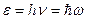и импульсом 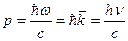. Фотон обладает целочисленным моментом s=1. Следовательно, фотоны подчиняются статистике Бозе-Эйнштейна – газ фотонов. Взаимодействие между фотонами отсутствует – газ идеальный. Равновесное излучение – фотонный газ в полости объёмом V.

Отличие фотонного газа от молекулярного – нельзя говорить о фиксированном числе частиц!! Фотоны могут создаваться или исчезать в процессе излучения и поглощения света. Покажем, что исходя из представлений о фотонном газе – газе фотонов – можно, используя (10) – распределение Бозе, получить формулу Планка.

Итак, воспользуемся сначала минимумом свободной энергии:

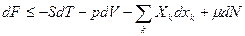
При T=const, V=const, X_k=const dF≤μdN, а в равновесии F минимально, то есть 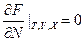, но 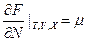и μ=0. Итак, μ=0

Теперь: 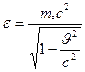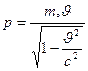и при 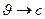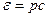(вместо )

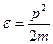Значит в формуле (10) 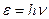и

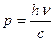
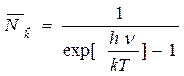(36)

Теперь формула для внутренней энергии:

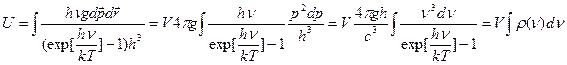
dε=cdp

Иначе – находим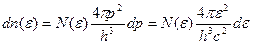

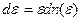
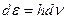
Итак, 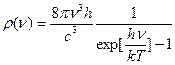(37) – формула Планка – результат Бозе-распределения с μ=0!!! (g=2 – две поляризации фотона в отличие от бозонов g=2s+1)

Ультрарелятивизм приводит к уравнению состояния pV=U/3→p=U/3V. Можно проверить, вычислив Ω.

Итак, провели «корпускулярный вывод» формулы Планка.

Условие «невырожденности» 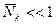здесь (μ=0):

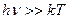
При этом – Больцмановская статистика.

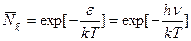- получаем формулу Вина

Полное число фотонов (в равновесии):

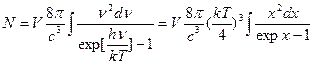(38) – зависит от T и V

Таким образом, «классическая статистика» к фотонному газу – входит 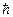, и область применимости 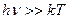. Это условие является обратным по сравнению с условием применимости классической статистики к осцилляторам электромагнитного поля. Посмотрим при 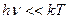- формула Рэлея-Джинса, и в неё не входит h (сильное вырождение для фотонного газа). Итак, при больших частотах (или низких температурах) – преобладают корпускулярные свойства, при низких частотах (или высоких температурах) – волновые свойства.

При волновом выводе была ещё энергия 0-х колебаний 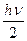, 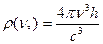. При корпускулярном выводе этого нет, так как фотоны полностью отсутствуют (N=0) – энергия вакуума.