Вырожденный Ферми-газ.

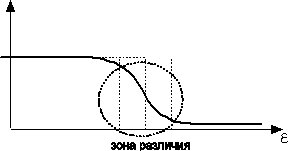
Обратимся теперь к Ферми-частицам. Условие нормировки и здесь даёт, что при уменьшении T (μ<0) |μ| растёт, при некотором T=T_выр μ=0. Однако здесь ничто не мешает μ стать положительным при 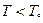(см. рис.). Рассмотрим сначала газ фермионов при T→0. Функция распределения даёт:

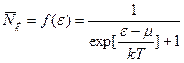(11)

При T→0 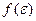стремится к единичной функции хевисаи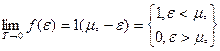де:

, где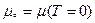

И видно, что 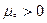, иначе частицам некуда деться

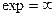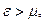
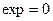при

при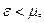

Здесь рисунок

Имеем в виду наиболее важные приложения, будем говорить об электронном газе g=2s+1=2, s=1/2. На каждом уровне в металле согласно принципу запрета Паули может находиться не более двух электронов с противоположно направленными спинами. Так как на нижнем (0-м уровне) – только два электрона, то 3-й и 4-й вынуждены занимать 1-й возбуждённый уровень, 5-й и 6-й – 2-й и т.д. Если полное число электронов N – то занятыми будут N/2 (или (N+1)/2) уровней с энергиями 0≤ε≤μ_°. Остальные уровни с ε≥ε_max – свободны. Таким образом, благодаря принципу запрета, электроны вынуждены попадать в возбуждённое состояние даже при абсолютном нуле температуры.

ε_max= μ_° - энергия Ферми. Найдём её из условия нормировки:

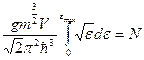
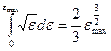
отсюда для электронов (g = 2) энергия Ферьми:

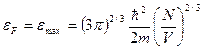(39)

Аналогичное «плотное заполнение» будет при Т = 0 и в пространстве импульсов – внутри сферы с радиусом p_max=(2mε)^1/2 – поверхность Ферми (при ε_i << m₀c²),

Полная внутренняя энергия, при Т = 0:

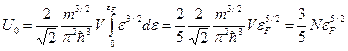(40)

Из уравнения состояния pV = 2U/3

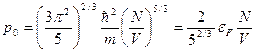(41)

Даже при Т= 0 давление ферми газа отлично от нуля.

В метане: N/V = 5*10²²cm^-3, p₀ = 5*10⁴atm

Формулы (40), (41) справедливы приближенно также при температурах близких к абсолютному нулю:

kT << ε_F; kT << 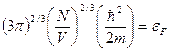(42

(T_F = ε_F/k), T_F по порядку величины, естественно, совпадает с температурой вырождения. Еще раз численная оценка: T_F~10⁴ 10⁵ (ε_F~10^-12 эрг). Т.е. электронный газ в металлах при любых Т, вплоть до Т плавления можно считать вырожденным. T_F – температура вырождения.

Электронный газ обладает своеобразной особенностью – он становится тем более идеальным, чем выше его плотность. Почему? Рассмотрим плазмы: электроны и ионы(ядра)(Наличие ядер не сказывается на ТД величинах электронного газа)

Энергия кулоновского взаимодействия электронов с ядрами, на один электрон: ze²/a, где ze – заряд ядра, а ~ 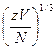- среднее расстояние от электрона до иона. Условие идеальности: энергия взаимодействия ze²/a ~ ε_F, ze²/a << ε_F. Подставим а и получим:

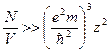- выполняется тем лучше, чем больше N/V.

Для невырожденного газа(обычной плазмы):

ze²/a << kT => 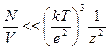- наоборот.

Практическое значение имеет выход электронов в теплоемкость металла. В 0-м приближении T << T_F C = 0: U₀(40) не зависит от Т. Но надо более подробно рассмотреть частицы в зоне разности, где ε(Т) – сущетсв. зависимость. По классической теории, если электроны в идеальном газе, то они должны в одновалентном газе (z = 1) давать в теплоемкость вклад 3R/2 – на эксперименте на два порядка меньше. Почему? Электронный газ сильно вырожден при обычных Т, и доля электронов дающих вклад в теплоемкость можно оценить, как отношение kT и ε_F:

С_e ~ (3R/2)(kT/ε_F).

Взяв за основу формулы (22) и (26):

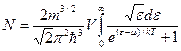
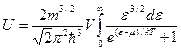
Попробуем получить результат более точно. Интегралы: 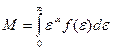(П1);

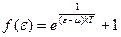– ф.р. Ферми

Пусть kT << μ

Интегрируем (П1) по частям:

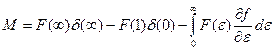(П2), где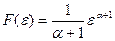

F(0) = 0, f(∞) = 0, и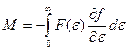

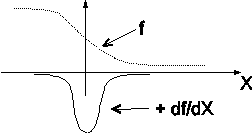
Перейдем к переменной x = (ε - μ)/kT:

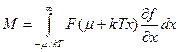, μ >> kT => нижний предел à -∞

Вклад дают только малые x

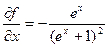- четная, острая

Тогда F(μ + kTx) в ряд Тейлора и берем несколько первых членов:

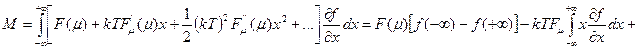
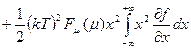
1) f(-∞) = 1; f(+∞) = 0;

2) 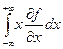= 0

3)

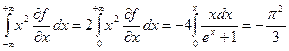
Итак, 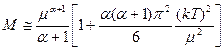(П4)

Тогда 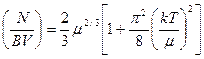(43)

При Т = 0, μ = μ₀ = ε_F

При Т ≠ 0 (43) можно переписать как:

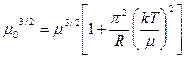, причем во втором слагаемом можно положить μ = μ₀, тогда с точностью до 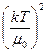, имеем:

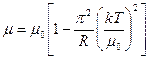(44)

Теперь положим 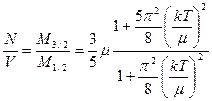, и с помощью (44) до ~ 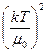имеем:

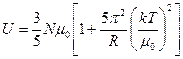(45)

и для теплоемкости идеального газа

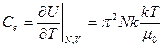(46)

С_e ~ T, à 0 при T à 0. Но С_реш ~ T³, и С_e > С_реш при T à 0.

Для вычисления энтропии вычислим Ω = -2U/3 = 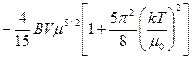(47)

Отсюда найдем энтропию:

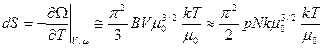(48)

И, наконец, найдем давление p = -Ω/V => 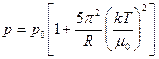(49)

Тепловое движение дает только маленькую добавку в давление электронного газа в металле.