Каноническое распределение Гиббса

Будем рассматривать систему, помещенную в термостат и дадим для нее выр-е вер-ти ее сост. При ТД равновесии. В класс. стат. для такой системы было канонич. распр. Гибса

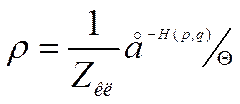(1)

будем полагать, что энергия системы может принимать дискретный ряд значений ε₀,ε₁,ε₂… ε_n каждому из которых соответствует определенное состояние системы описываемое определенной волновой функцией. (В кв. механике все значения ε разрешены). Как видоизменится каноническое распределение? Функцию гамильтониана Н(p,q) заменить оператором:

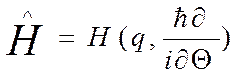
Матрица пл-ти(аналог пл-ти вер-ти)для квсистем запишется как:

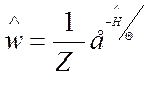(2)

Определим в энергетическом представлении диагональные(только они отличные от 0 )элементы матрица объема пл-ти

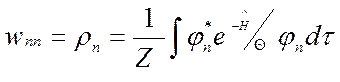
φ_n –полная система ортонормированных ф-ий оператора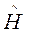

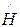φ_n= ε_n φ_n

ε_n-собственное значение Н

так как

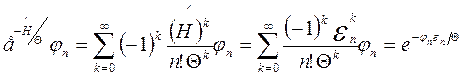
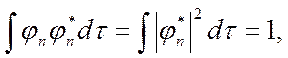,то для квантового канонического распределения Гиббса имеем:

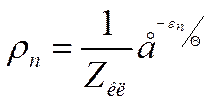(3)

где ρ_n - вер-ть найти систему в квант сост с энергией ε_n

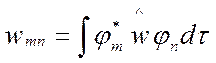
Матрицу пл-ти 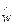в энергетическом представлении (3) часто называют статистической матрицей. Условие нормировки для (3) имеет вид:

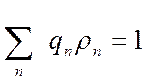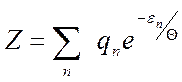,или (4)

Z- стат сумма(был стат. интеграл) q_n –кратность вырождения уровней(используем постулат о равновероятности у ровней с аддитивной энергией) и (называют стат весом анологичноΩ(ε))

Свободная энергия

Было: 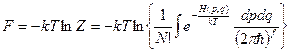(5)

Утверждение было что такое интегрирование эквивалентно суммированию по всем возможным микросост. В квантовой статистике естественно подZ понимают стат. сумму в (5)

(5’)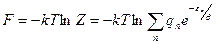

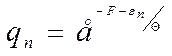(6)

вычислим среднее значение энергии

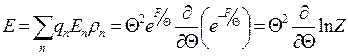
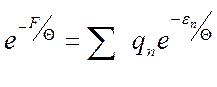
Энтропия

Было определение:(41), л.3 или 4

S=klnΔГ и аппроксимировали

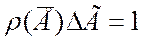,приходили к формуле для энтропии

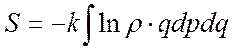
Проделав все аналогично получим:

S=-klnρ_n(E_n)

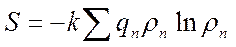(8)

Но теперь ΔГ – число возможных квантовых состояний,соотв разбросу энергии ΔЕ в канонич распр (3)

Теперь возьмем

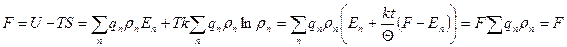
что и должно быть.