Третье начало термодинамики (принцип Нернста 1906г)

сформулирован в рез-те исследований свойств тел при низких Т- это и есть область применимости. Почему сейчас – обосновывается только с пом кв стат?

итак

при прибл к абсолютному нулю энтропия всякой равновесной системы стремиться к одному и тому же для всех систем конечному значению, которое можно положить равным нулю.

Это происходит независимо от любых ТД параметров сист, как внеш, так внутр, и lim_T→0[S(T,x₂)-S(T,x₁)]=0 (1)

lim_T→0∂S/∂x|_T=0 (2)

x-любой параметр, раньше энтропия определялась с точностью до Cоnst и имела смысл только разность энтропий

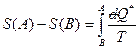(3)

если теперь в (3) за состояние (B)выбрать ситстему при Т=0 то можно положить S(В)=0.

Существенным здесь является не то что S(В)=0 а то что ее величина не зависит от того каковы значения внешних параметров системы в сост В. По скольку для всех систем S одинак – естественно принять

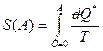(3*)

Т.О.(важно) при Т=0 изотерма и адиабата совпадают

dQ*=dU+∑Xidxi

при низких температурах, отметим, охлаждение уже нельзя осуществить за счет просто отдачи тепла холодильнику, а только за счет убыли внутр энерг при адиабатическом расшир (соверш А)

Охлажд системы таким образом осущ повторением следующих друг за другом пр-сов адиабатического расширения(при котором снимается Т) и изотерм сжимание(уменьш S) по третьему закону при Т стремящемся к нулю S перестает изменяться. Поэтому законечное число указанных процессов состояние с S=0 недостижимо, а следовательно недостижим и 0К. К 0К можно лишь асимптотически приближаться !!!!!!

0К недостижим. Это эквивалентно формулировке 3го начала ТД

Так Нерист и формулировал

Следствия:

1) С стремиться к 0

Действительно C=T∂S/∂T₌∂S/∂lnT

S- конечно(→0) а lnT→∞( T→0), и С→0(4)

В Базарове рассмотрено по др там показано что С~T^α,α>0на основе ф-лы(4)

2) тепловой коэфициент

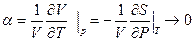по скольку S стремится к нулю а давление конечно

3) термически коэф давления стрем к 0

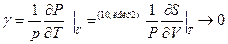по 3му началу

4) если известна теплоемкость Сr то можно вычислить энтропию однозначно

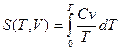
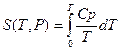(4)

от сюда поскольку S →0 при T→0 Сp , Cv ~ T^α,α>0? Чтобы интенсивность сходилась

именно по этому проблема теплоемкости занимала такое важное место в физике в начале ХХ века занимались Эйнштейн ДеБай, Борн и др

В класс стат обосновать 3е начало не удается при T→0 работают квантовые св-ва тел что дает квантовой статистике известно((7),л2)

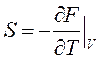далее F=-kTlnZ

Z- стат сумма Z=∑_nq_nexp(-ε_n/kT) т.о. S=k∂(TlnZ)/∂T (5) и .

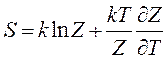(5`) с другой стороны

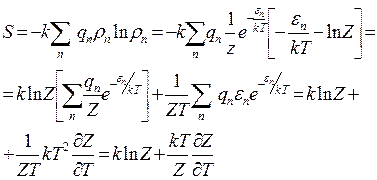
(пришли к тому же что и 5` а как же еще)

Теперь!!! (Где раб кв. стат) при T→0 εkT<<ε1-ε0

ε0- начальный уровень

и

Z=∑_nq_nexp(-ε_n/kT) ≈q₀exp(-ε₀/kT) (!!!!!!!) продифференцируем

S=S₀=klnq₀ (6)при T→0

Если основной (нулевой) уровень

Не вырожден(q₀=1) то S₀=0!!! Принцип Нериста но утверждать это нельзя однозначно. Если ρ₀≤N (N число частиц в системе) то S₀=klnN. при обычных температурах S~kN и S₀/S~(lnN)/N<<<<1 исч. для макро систем. только если q₀~e^N S₀/S~1 однако физ сист с таким q₀ не известны

Квантовая сист. не взаимод. тождейств. частич. До сих пор при квантовом рассмотрении учитывали только дискретность энергии спектра. Есть еще одна квантовая особенность тождественных, одинаковых частиц – их принцип. неразличимость (использовали для разрешения порадокса Гиббса). Если не учитывать то например уже Т~0.0004К

Электроны должны подчиняться класс. стат. М-Б

Что приводит к рез. Против. Данным экспер. (По теплоемкости металлов). Нужна другая специфическая кв. стат. – это стат. Бозе (для частиц описыв. Симметр. Волнов. Ф-ции , они обладают целым спином. Сколько угодно таких частиц может находиться в одном кв. сост. ) и И статистика Ферми(антисимметричная волновая ф-я частицы с полу целым спином, действует принцип Паули: 2 частицы не могут одновременно находится в одном и том же кв сост) получили распр Бозе и Ферми основа