Равновесное излучение

Характерное излучение э/м волн (света), его интенсивность зав-ть интенсивности от частоты (спектральный состав изл.) – зависят, вообще говоря, от природы изл-его тела, и от его температуры. Имеется однако,случай, когда спектральный состав изл-я не зависит от природы изл. и опр-ся только его температурой. Речь идет о равновесном изл-ии. Представим себе некотор замкнутую полость, со стенками не провод тепла и поддерживаемыми при опр температуре Т. Стенки этиой полости будут излучать и насыщать э/м волны. Через нектор время (полость замкнута) – в системе установилось ТД стат равновесие. Пл-ть энерг. Этого излуч. w=w(ν,T) (ν-частота)при этом (можно показать из 2го нач ТД), что w(ν,T) не зависит от природы излучателя(стенок) Действительно если полостей 2, с различными w приодинаковой Т то можем объединить полости. Равновесие нарушим таким образом в этой части, где w была меньше – излуч будет переходить туда. Плотность изл здесь возрастет, сл-но поглощение в стенках возрастет, сл-но Т возрастет, сл-но возникнет разность Т которую впринципе можно использовать для получения работы(самопроизвольное нарушение равновесия – противоречит 2му началу)

Т.О. – w(ν,T)-универсальная формула. ТД равновесное излучение – занимались на практике(З-н Стефана Больцмана получили).Можно получить использую классическую статистику w(ν,T) Но сразу в квантовой а потом обсудим и классическую

Рассмотрим волн. Ур-е для э/м поля

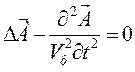(12)

(пусть далее Vф=C – считаем что полость - вакуум)

Пусть размер велик >>>>>>>> λ (12) – справедливо в обл. где нет зарядов и токов. На границе полости надо задавать гр. усл. И источники но они интегрируются обычно внутри. Разобьем всю область пр-ва своб. От зарядов на совокупность кубов (нормировочных) размером L и рассмотрим поле внутри одного куба тогда надо задать гр. усл. На пов-ти этого куба. э/м поле предст. собой совокупн. бегущих волн. Решение виде бегущих волн возникнет, если принять, что 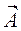и его производные имеют равные зн-я на противоположных границах куба. Это эквивалентно требованию периодичности граничных условий

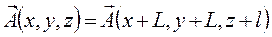(13)

(L>>λ) Если решим (12) с гр.усл.(13), то – во всем пр-ве легко простым периодичн. Повторением

Решение ищем виде:

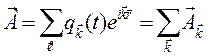(14)

(k=2П/ λ=w/c) (более общ: 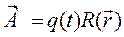) и разделим переменные как матфизика

(14)→(12) имеем: 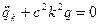(15)-ур-е осциллятора, с w=ck т.о. э/м поле- набор осцилляторов. Для того чтобы вычислить w(ν,T) надо знать сколько их (w=2пν)приходится на интервал частот (w,w+dw) (или – по сколько есть связь w и k → Диск. Ур. → на интервал k, k+dk) из (13) и (14) ясно, что вектора кмогут принимать дискретный ряд значений

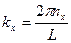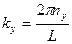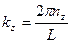; ; (16)

n_x n_y n_z = 0,1,2.....- целые

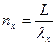
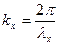
Далее 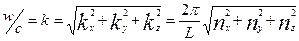(17)

Итак число осцилляторов рано, очевидно числу бегущих волн. В каждой тройке чисел n_x n_y n_z соотв. опр число к которое опр. (17)! Сл-но число волн (осцилляторов), в системе (к,к+dk) равно числу чисел n=kL/2п, (см(17)), лехащих в интервале между n и n+dn, а это узкая сфера и для этого числа имеем, очевидно значение

q(n)dn=4πn²dn (18)

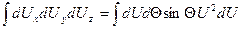
т.о.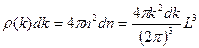

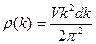(19)

или переходя, к циклическим частотам

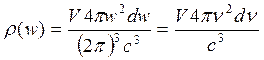(20)

Ф-лу (20) надо уточнить. 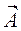-вектор и есть, как известно 2е незав. Поляризации, поэтому прав. часть(20) , надо умнож на 2! Число незав. Осц. Надо удвоить имеем

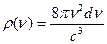(21)-пл-ть числа осц. в ед. объема.А плотность энерг? Надо умнож на 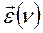из(11) имеем: пренебрегая 0-ми колеб.

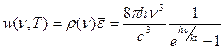(22)- ф-ла Планка 1900г декабрь

Здесь не учтена эн нулевых колеб. Для каждой частоты она принята за начало отсчета при Т=0

Классический предел hν<<kT, 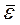=kT как и было в классике

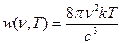(23)- ф-ла Релея-Джинса июль 1900г

эта ф-ла была получена раньше. Ясно что 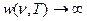при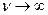

и инт.∫w(ν,T)dν расходится(ультрофиолетовая катострофа, катострофа Релея-Джинса) С пом. кв. теор.предложенной Планком – разрешается

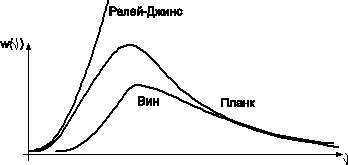
При hν>>kT

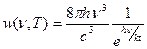(23) – ф-ла Вина

Проинт теперь (22) по dν, найдем полн. внут. энерг.

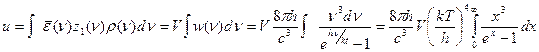(24)

μ=σТ⁴V закон Стефана-Больцмана

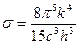постоянная Стефана-Больцмана

на практике используя р=1/3w(из Эл.динамики) получили (24) с использ первого следствия

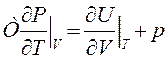
если учесть 0-е колеб в (11) то U расходится . а Планк прекрасно согласуется с эксперементом????? Это одна из проблем кв. Эл.динамики почему не надо учит нулевые колеб

теперь идем на оборот

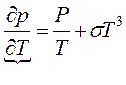-д.у. решаем методом вариации произв пост, имеем

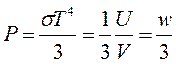Ур. Сост ид. Фотонного газа